Zajęcia 6

Wnioskowanie w KMNRL III

Model liniowy

Podsumowanie zajęć poprzednich / Wprowadzenie

Na ćwiczeniach i laboratoriach zajmowaliśmy się stosowaniem wybranych technik wnioskowania dostępnych w KMNRL; a dokładniej łącznym wnioskowaniem o wielu parametrach czyli testem F w szczególnej postaci testowania istotności (łącznego zerowania) kilku współczynników regresji.

W niniejszych zajęciach najpierw przedstawiona zostanie pogłębiona analiza możliwości modelu liniowego pokazująca, jak można go „uogólnić” by otrzymać lepsze możliwości opisu zależności między zmiennymi, następnie omówione będzie wnioskowanie o liniowych kombinacjach parametrów regresji, którego potrzeba wynika między innymi właśnie z takiego „uogólnienia”.

Ponadto (jako materiał dodatkowy, uzupełniający) przedstawiona zostanie ogólna wersja testu F służąca do łącznego testowania kilku liniowych restrykcji dla parametrów regresji.

Zajęcia 6

Celem zajęć jest przećwiczenie wnioskowania o liniowej kombinacji parametrów regresji oraz pogłębione przedstawienie możliwości modelu liniowego

W Klasycznym Modelu Normalnej Regresji Liniowej posługujemy się pewną szczególną zależnością między rozważanymi zmiennymi a nieznanymi parametrami: postacią liniową (ze względu na parametry). Modele liniowe mają w ekonometrii podstawowe znaczenie – wiele użytecznych twierdzeń udowodniono korzystając z liniowej postaci modelu; ich „nieliniowe” odpowiedniki mają często słabszą tezę lub wymagają silniejszych założeń. W modelu liniowym dysponujemy ponadto bezpośrednio danymi (analitycznymi) rozwiązaniami postawionych w definicjach kryteriów, np. estymator Metody Najmniejszych Kwadratów ma daną wprost postać analityczną, ponieważ (jak pokazaliśmy) dla modelu liniowego można explicite rozwiązać zagadnienie minimalizacji sumy kwadratów reszt i podać gotowy wzór. W modelach nieliniowych kryterium definiujące estymator może być ogólnie zadane lecz jego realizacja może wymagać np. zastosowania algorytmu numerycznego, co jest źródłem dodatkowych trudności. Model liniowy ma więc lepsze własności zarówno teoretyczne, jak i techniczne (dotyczące realizacji numerycznej).

Wobec tego model liniowy zawsze będzie punktem odniesienia dla alternatywnych form; w związku z tym należy szczegółowo rozważyć jego możliwości i ograniczenia.

Zajęcia 2 oraz Zajęcia 3 poświęcone są modelowi liniowemu w najprostszej wersji. Pokazane są tam podstawowe własności modelu oraz sposoby interpretowania ocen parametrów. Warto jednak dokładniej rozważyć zagadnienie:

Jaki rodzaj zależności pomiędzy zmiennymi możemy badać przy pomocy modelu liniowego?

Oczywiście odpowiedź: „zależność liniową!” jest zbyt trywialna żeby była prawdziwa. Aby zająć się tym zagadnieniem, użyteczne będzie wprowadzenie rozróżnienia pomiędzy: zmiennymi w regresji a wielkościami ekonomicznymi.

ZMIENNĄ W REGRESJI nazwijmy to, co stoi przy parametrze (czyli wartości z i-tej kolumny macierzy X)

WIELKOŚCIĄ EKONOMICZNĄ nazwijmy wyrażoną liczbowo wielkość mającą interpretację ekonomiczną (jak np. stopa inflacji, wielkość PKB, stopa procentowa, wielkość wydatków na żywność w gospodarstwie domowym, etc.

Zauważmy, że model liniowy wymusza uproszczoną postać zależności zmiennych w regresji, gdy tymczasem ekonomista jest zainteresowany badaniem i interpretacją zależności pomiędzy wielkościami ekonomicznymi.

Jeżeli zmienne w regresji utożsamimy z wielkościami ekonomicznymi (i nazwiemy po prostu zmiennymi), to możliwości modelu liniowego będą dość mizerne:

- wpływ zmiennej objaśniającej na objaśnianą jest „zawsze taki sam”: nie zależy ani od poziomu rozważanej zmiennej objaśniającej...

(czyli nie jest możliwa sytuacja gdy jakiś czynnik ma w małej ilości wpływ silny a w większej ilości coraz słabszy)

[gdy rozważamy wpływ liczby lat edukacji szkolnej na wydajność pracownika, to wzrost łącznego czasu nauki z 1 roku do 2 lat ma taki sam wpływ na wydajność jak wzrost z 40 lat na 41 lat nauki J

- ...ani od poziomów pozostałych zmiennych objaśniających.

(czyli wpływ zmiennych objaśniających jest „addytywnie separowalny”)

jeśli rozważamy oczekiwaną cenę samochodu jako funkcję parametrów technicznych, to np. wzrost mocy silnika podniesie cenę tak samo niezależnie od tego czy samochód ma drogę hamowania 200 metrów czy 45 metrów.

Gdy jednak zrezygnujemy z utożsamiania zmiennych w regresji i wielkości ekonomicznych okaże się, że jeśli idzie o zależność między wielkościami ekonomicznymi możemy uwolnić się od powyższych ograniczeń zachowując przy tym zasadnicze zalety wynikające z liniowej postaci modelu. Wystarczy, że wprowadzimy do modelu wiele zmiennych w regresji będących nieliniowymi funkcjami niewielu wielkości ekonomicznych. Możemy rozważyć:

1. Obok zmiennej w regresji „poziom wielkości ekonomicznej A” wprowadzenie zmiennej w regresji „kwadrat poziomu A” – wtedy przy A i A² możemy uzyskać np. oceny parametrów o odmiennych znakach. Dla niewielkich poziomów A zmienna „poziom A” będzie dominująca, ze wzrostem A, zmienna „kwadrat poziomu A” zacznie przeważać – dzięki temu możemy odzwierciedlać wpływ wielkości ekonomicznej A na zmienną objaśnianą zależny od poziomu A.

2. Jeśli mamy dwie wielkości ekonomiczne, A i B, możemy wprowadzić dodatkowo zmienną w regresji „A razy B” – wtedy parametr przy takiej zmiennej będzie odzwierciedlał zależności między tymi wielkościami – wpływ jednej będzie zależał także od poziomu drugiej.

Zamiast rozważać regresję:

(1) y_t= a₀ + a₁ z_t + a₂ v_t + e_t

rozważmy:

(2) y_t= a₀ + a₁ z_t + a₂ z_t ²+a₃ v_t + a₄ v_t ²+ a₅ z_t v_t + e_t

W ten sposób wprowadzając np. kwadraty i iloczyny podstawowych wielkości, możemy uzyskać model który dużo bardziej subtelnie odzwierciedla zależności pomiędzy rozważanymi wielkościami. W ekonometrii często rozważa się logarytm (np. naturalny lub dziesiętny) [a czasem pierwiastek] wielkości ekonomicznych: wielkości ekonomiczne zwykle są dodatnie i dają się logarytmować.

Wtedy w regresji mamy kwadraty i iloczyny logarytmów wielkości ekonomicznych.

Do regresji możemy wprowadzić wyłącznie nieliniowe funkcje wielkości ekonomicznych – wykorzystanie kombinacji liniowych spowodowałoby niespełnienie założenia o rzędzie macierzy X [nie możemy rozważać modelu w którym mamy: ...+ a₁ ln z_t + a₂ ln (z_t ²) ponieważ jest on równoznaczny z: ..+ a₁ ln z_t + a₂ 2 ln z_t+ .... i nie spełnia założenia 3 KMRL; natomiast model + a₁ ln z_t + a₂ (ln z_t)² +.. jest OK. ]

Jednak takie ujęcie powoduje też pewne niedogodności. Musimy szacować więcej parametrów; oraz co ważniejsze musimy zmienić ich interpretacje. Nie możemy już używać standardowej interpretacji:

„Wielkość a_i mówi nam o ile jednostek wzrośnie/spadnie w przybliżeniu wartość zmiennej objaśnianej gdy wartość i-tej zmiennej objaśniającej wzrośnie o 1 jednostkę przy niezmienionych wartościach pozostałych zmiennych”

ponieważ nie zachodzi ostatni warunek: „...przy niezmienionych wartościach pozostałych zmiennych”. Nie może on być spełniony, bo jak ma wzrosnąć A przy niezmienionej wartości A² i AB?

Stosując tu omówione rozszerzenie modelu tracimy zwykle interpretowalność poszczególnych współczynników regresji – wartości ich ocen same w sobie nic nam nie mówią. Czy to duża strata? Zastanówmy się, na czym naprawdę nam zależy. Zwykle chcemy znać pewne charakterystyki wiążące badane wielkości ekonomiczne, np. elastyczności. Możemy być zainteresowani badaniem o ile % zmieni się badana wielkość ekonomiczna W gdy wielkość H zmieni się o 1% przy niezmienionych wielkościach pozostałych zmiennych (to standardowa interpretacja elastyczności). Elastyczność „W po H” jest zdefiniowana jako:

Ostatnia równość wykorzystuje tzw. pochodną logarytmiczną – jest to tożsamość wynikająca z rachunku różniczkowego (oczywiście odpowiednie logarytmy muszą istnieć). Gdy rozważamy model:

(3) ln y_t= a₀ + a₁ ln z_t + a₂ ln² z_t+a₃ ln v_t + a₄ ln² v_t + a₅ ln z_t ln v_t + e_t

[ln²z_t oznacza (ln z_t)² ]

okaże się, że elastyczność y_t po z_t jest dana wzorem (zgodnie z ostatnią równością):

El yt/zt = a₁ + 2 a₂ ln z_t + a₅ ln v_t

Jeżeli wartości z_t oraz v_t potraktujemy (zgodnie z 2 zał. KMRL) jako pewne stałe, badana elastyczność okaże się liniową kombinacją parametrów regresji [ze znanymi współczynnikami]. Jest to przejaw ogólniejszej prawidłowości:

Gdy rozszerzymy model według opisanego powyżej schematu, tracimy co prawda interpretowalność pojedynczych parametrów regresji, ale zwykle okazuje się, że z ekonomicznego punktu widzenia interesują nas (i podlegają interpretacji) pewne funkcje parametrów (często liniowe). Oznacza to, że szczególnie będą nas interesować techniki wnioskowania statystycznego o pewnych funkcjach (a nie tylko bezpośrednio o wartościach) nieznanych parametrów regresji. Poniżej podany zostanie sposób wnioskowania statystycznego o liniowych funkcjach (liniowych kombinacjach) parametrów regresji.

WNIOSKOWANIE O LINIOWEJ KOMBINACJI PARAMETRÓW

W KMNRL estymator MNK parametrów regresji b^ ma k-wymiarowy rozkład normalny o wartości oczekiwanej równej nieznanym parametrom b [jest nieobciążony] i macierzy kowariancji s²(X’X)^-1. Pozwala nam to (jak opisano lub zasygnalizowano w wykładach) wyprowadzić rozkłady odpowiednich statystyk testowych i w konsekwencji przeprowadzać testy i konstruować przedziały ufności. Jeżeli rozważymy kombinację liniową parametrów regresji ze stałymi (nielosowymi) współczynnikami, to zgodnie z własnościami rozkładu normalnego (por. rozkłady związane z normalnym punkt I C) ma ona również rozkład normalny o odpowiednio zadanych parametrach. O nowym parametrze będącym liniową funkcją oryginalnych parametrów regresji b możemy więc wnioskować w analogiczny sposób jak opisano w poprzednich zajęciach.

Przyjmijmy założenia KMNRL oraz oznaczenia:

b – wektor nieznanych parametrów regresji

b^ -estymator MNK tych parametrów

interesuje nas skalarny parametr:

g = c’b

wektor-kolumna c grupuje pewne stałe - współczynniki rozważanej kombinacji liniowej.

Rozważamy parę hipotez:

H₀: c’b = r* ; H₁: c’b ¹ r*;

[gdzie r* to pewna stała - testowana wartość]

co zapisujemy równoważnie jako:

H₀: g = g* ; H₁: g ¹ g*;

[gdzie g* to pewna testowana wartość]

podstawiając c’b = g oraz r*= g*

następnie cały poznany mechanizm testu t stosujemy do g, dzięki czemu możemy wnioskować o liniowej kombinacji parametrów regresji.

Wtedy:

g^ = c’b^

[ocena parametru gamma to c’ razy oceny współczynników regresji b^]

V(g^) = c’V(b^)c = s²c’(X’X)^-1c

[macierz kowariancji estymatora parametru g - (por. rozkłady związane z normalnym punkt I C; c’ to macierz A w zapisie tam stosowanym, powyżej s² jest jako skalar wyciągnięte na początek formuły)]

V^(g^) = c’V^(b^)c = s²c’(X’X)^-1c

[ocena macierzy kowariancji estymatora parametru g]

D(g^) = [c’V^(b^)c]^0,5 = [s²c’(X’X)^-1c]^0,5

(^0.5 czyli potęga 0,5 to pierwiastek kwadratowy) [tu mamy błąd średni szacunku g]

mając g^ oraz D(g^) możemy stosować wnioskowanie o nieznanym parametrze regresji takie jak opisane w Zajęciach 4 – testować hipotezy o g testem t oraz budować dla g przedziały ufności (tylko zamiast b_i wszędzie bierzemy g).

Żeby docenić znaczenie tej możliwości trzeba uświadomić jak wiele można sprowadzić do zapisu g = c’b. W zastosowaniach najistotniejsze jest prawidłowe zbudowanie wektora c i obliczenie błędu średniego szacunku szukanej kombinacji czyli D(g^). Poniżej są przedstawione przykłady. Rozważmy jednak najpierw najprostszy szczególny przypadek, gdy g = b_i ; chcemy więc znaleźć błąd średni szacunku i-tego parametru regresji. Wektor c zawiera wtedy jedynkę na i-tym miejscu oraz same zera poza tym. Zastosowanie wzoru c’V^(b^)c odpowiada wybraniu i-tego elementu przekątniowego z oszacowanej macierzy kowariancji b^ - pierwiastek z tego elementu to błąd średni szacunku g = b_i – stosując przedstawiany tu wzór uzyskujemy więc zgodność ze znanym już sposobem wyliczania D(b_i^).

Przykłady konstrukcji wektora c:

1. Wnioskowanie o sumie parametrów regresji.

Przypuśćmy, że mając oszacowane równanie regresji:

y_t^ = b₀^ + b₁^x_t1 +b₂^x_t2 +b₃^x_t3

chcemy wnioskować o sumie dwóch parametrów b₁ + b₂ . Wtedy oszacowanie takiej sumy to oczywiście suma oszacowań (choć jest w tym głębsza teoria) czyli b₁^ + b₂^. Do testowania testem t lub konstrukcji przedziału ufności potrzebujemy jeszcze błędu średniego szacunku tej sumy. Uwaga! Ogólnie D(b₁^ + b₂^) to NIE jest D(b₁^) + D(b₂^)!!!

Aby obliczyć D(b₁^ + b₂^) trzeba zastosować podane wyżej wzory. Do tego potrzebujemy postaci wektora c. Zasada jego konstrukcji jest następująca: zapisujemy rozważany wzór uwzględniając WSZYSTKIE parametry regresji i do wektora c bierzemy wszystko POZA samymi b. W tym wypadku:

g = b₁ + b₂ = 0 * b₀ + 1 * b₁ + 1 * b₂ + 0 * b₃

czyli wektor c ma postać: [podaję c’ żeby się mieściło w linii]

c’ = [ 0 1 1 0]

Wtedy rzeczywiście g = c’b = b₁ + b₂

Mając policzone wcześniej s²(X’X)^-1 liczymy tylko c’s²(X’X)^-1c i bierzemy z tego pierwiastek i mamy D(b₁^ + b₂^). Uwaga! c musi mieć tyle wierszy ile kolumn ma X oraz (X’X)^-1 i oczywiście zakładamy, że kolejność kolumn w X jest odpowiednia do tego jak konstruujemy c.

W przykładach często może się okazać, że błąd średni szacunku sumy parametrów jest znacznie mniejszy niż błąd średni szacunku każdego parametru osobno. Oznacza to, że suma tych parametrów jest precyzyjniej szacowana, a sposób dekompozycji tej sumy na dwa parametry jest już obciążony większą niepewnością.

2. Testowanie hipotezy o równości dwóch parametrów regresji.

Czasem chcemy weryfikować hipotezę mówiącą, że wartość dwóch parametrów jest taka sama – może to odpowiadać „zapytaniu”, czy wpływ dwóch zmiennych objaśnianych na zmienną objaśniającą jest taki sam, czy istotnie inny.

W modelu popytu na wieprzowinę o postaci:

ln D_t= a₀ + a₁ ln P_t + a₂ ln Y_t + a₃ ln Pr_t + a₄ ln Pd_t + a₅ ln Pw_t + e_t

D – to wielkość popytu na wieprzowinę,

P – cena wieprzowiny

Y – dochód dyspozycyjny

Pw – cena wołowiny

Pr – cena ryb

Pd – cena drobiu

Możemy testować np. hipotezę, że dwie elastyczności cenowe mieszane (tj. względem ceny innego dobra) popytu są sobie równe – np, że wielkość popytu na wieprzowinę tak samo reaguje na zmiany ceny ryb jak na zmianę ceny drobiu.

Testowana para hipotez mogłaby mieć tu postać:

H₀: El _D/Pr = El _D/Pd ; H₁: El _D/Pr ¹ El _D/Pd ;

co odpowiada w naszym modelu hipotezom:

H₀: a₄ = a₅ ; H₁: a₄ ¹ a₅ ; (stosując wzór z pochodną logarytmiczną łatwo możemy pokazać, że El _D/Pr = a₄ itd.)

co z kolei można zapisać jako:

H₀: a₄ – a₅ = 0; H₁: a₄ – a₅ ¹ 0 ;

jeżeli przyjmiemy:

g = a₄ – a₅

otrzymamy standardową parę hipotez dla parametru g:

H₀: g = 0; H₁: g ¹ 0 ;

Dla jej testowania posłużymy się statystyką testową t o postaci :

t_g= g^ / D(g^)

i dalej postępujemy standardowo, tylko potrzebujemy w tym celu wartości g^ i D(g^)

aby je otrzymać, musimy zapisać g = c’b

w tym przypadku ponieważ g = a₄ – a₅,

g = a₄ – a₅ = 0*a₀ + 0*a₁ + 0*a₂ + 0*a₃ + 1*a₄ + (-1)*a₅

c’= [ 0 0 0 0 1 -1]

stosujemy wzory:

g^ = c’b^

D(g^) = [s²c’(X’X)^-1c]^0,5

i dalej standardowo testujemy naszą hipotezę, otrzymując np. konkluzję : na poziomie istotności 0,05 elastyczność popytu na wieprzowinę względem ceny drobiu jest istotnie różna od elastyczności popytu na wieprzowinę względem ceny ryb.

3. Wnioskowanie o przykładowej kombinacji: g = 3b₀ + 1,5b₃.

(zakładamy, że równanie regresji ma postać jak powyżej). Postać wektora c w tym przykładzie to:

c’ = [3 0 0 1,5]

[wszystkie wzory jak wyżej]

Zauważmy, że wektor c ma grupować stałe – a na mocy 2 założenia KMNRL zmienne objaśniające X traktujemy jak pewne stałe, więc wartości zmiennych objaśniających mogą być parametrami badanej kombinacji.

4. Wnioskowanie o elastyczności w modelu (3) danym powyżej.

Rozważmy podany powyżej przykład modelu (3), gdzie:

ln y_t= a₀ + a₁ ln z_t + a₂ ln² z_t+a₃ ln v_t + a₄ ln² v_t + a₅ ln z_t ln v_t + e_t

gdzie elastyczność y_t po z_t jest dana wzorem:

El yt/zt = a₁ + 2 a₂ ln z_t + a₅ ln v_t

Gdybyśmy chcieli wnioskować o podanej elastyczności, to odpowiedni wektor c miałby postać:

c’ = [0 1 2 ln z_t 0 0 ln v_t]

5. Wnioskowanie o teoretycznej wartości zmiennej objaśnianej y^

Zauważmy, że wartość teoretyczna zmiennej objaśnianej czyli y^ jest (w modelu liniowym) liniową kombinacją współczynników regresji. O y^ możemy więc analogicznie wnioskować – testować testem t oraz budować przedziały ufności. W tym celu musimy znaleźć D(y^). Zauważmy, że

y_t^ = x_tb^

gdzie x_t to po prostu wiersz z macierzy X – z tego wzoru widać, że musimy przyjąć c’= x_t. Oczywiście wektor x_t może grupować dowolne, hipotetyczne – niekoniecznie pochodzące z rzeczywistych danych – wartości zmiennych objaśniających. W modelu (3) powyżej, wektor c dla wnioskowania o y^ (którym jest tam ln y_t – zachodzi mały konflikt oznaczeń) miałby postać:

c’ = [1 ln z_t ln² z_t ln v_t ln² v_t ln z_t ln v_t]

Tu wnioskujemy o teoretycznej (przewidywanej przez model) wartości zmiennej objaśnianej gdy zmienne objaśniające [zmienne w regresji] przyjmą wartości odpowiadające pewnym wielkościom ekonomicznym wynoszącym z_t i v_t.

UWAGA DLA MIŁOŚNIKÓW ŚCISŁEJ NOTACJI: tu przyjmujemy pewne uproszczenie: nie rozróżniamy nieznanej wielkości i jej oszacowania nazywając jedno i drugie y teoretycznym. De facto mamy nieznaną (w KMNRL nielosową) wielkość „y deterministycznego” = x_tb i jej oszacowanie (zmienną losową) = x_t b^. Ale żeby nie mnożyć notacji – bo trzeba by jakiś nowy symbol dopisać do y_t żeby oznaczyć x_tb – nazywamy tu wszystko to „y teoretycznym”. Mówiąc ściśle, test i przedział ufności konstruowalibyśmy dla nieznanej wartości „y deterministycznego” ale jako ekonometrycy możemy sobie pozwolić na trochę nieścisłości pod warunkiem, że jesteśmy jej świadomi. Możemy też powiedzieć (ściśle), że wnioskujemy o wartości oczekiwanej y_t:

zgodnie z pierwszym założeniem KMRL: E(y_t) = E(x_tb + e_t) = E(x_tb) + E(e_t) = x_tb + 0

i stosujemy w tym celu jej oszacowanie Xb^.

Wpływ skalowania zmiennej objaśniającej na błąd średni szacunku parametru

W Zajęciach 3 zajmowaliśmy się badaniem, jak zmieni się ocena MNK parametru kiedy stojącą przy nim zmienną w regresji (kolumnę X ) przeskalujemy p razy. Pokazano tam, że przemnożenie zmiennej objaśniającej w regresji razy p powoduje przemnożenie oceny parametru razy 1/p w porównaniu z sytuacją wyjściową. Możemy teraz zapytać jak zmieni się błąd średni szacunku tego parametru?

Przemnożenie oceny parametru razy 1/p odpowiada wektorowi c mającemu 1/p na i-tym miejscu a poza tym zawierającym zera. Jeśli takim wektorem obłożymy ocenę macierzy kowariancji estymatora MNK, to wybrany zostanie z niej tylko jej i-ty element przekątniowy oraz będzie pomnożony przez 1/p², zaś pierwiastek z tego (czyli właśnie szukany błąd średni szacunku parametru) będzie to błąd oryginalnego parametru razy 1/p. Stwierdziliśmy więc, że jeśli skalujemy i-tą zmienną objaśniającą (razy p), to oszacowanie stojącego przy niej parametru skaluje się tak samo jak jego błąd średni szacunku - razy (1/p). Wobec tego statystyka testowa typu t dla badania istotności tej zmiennej [czyli zerowania parametru], tzw. t-ratio [czyli ocena parametru przez błąd średni szacunku] nie ulegnie zmianie, bo zarówno licznik jak mianownik przemnoży się razy 1/p co się uprości. Widzimy stąd, że skalowanie zmiennej objaśniającej nie wpływa na wynik testu istotności stojącego przy niej parametru.

Sposób postępowania w zadaniach:

W zadaniu najważniejsze jest dobre wyspecyfikowanie wektora c - powyżej podano stosowne przykłady. Zawsze trzeba sobie wyliczyć c’b i zobaczyć, czy rzeczywiście wychodzi to, co chcemy, żeby wyszło. Równie ważne jest jednak sprawne wykonanie obliczeń – żeby nie dodawać sobie niepotrzebnej roboty. Przykładowo: zwykle w zadaniu dysponujemy macierzą (X’X)^-1 – jest dana lub wyliczyliśmy ją sami. Kiedy mamy odpowiedni wektor c, to aby wyliczyć V^(g^) = c’V^(b^)c najpierw policzmy c’(X’X)^-1c a dopiero potem (wynik ma wymiar 1 na 1) pomnóżmy to przez s² . Zdarza się, że niektórzy stosują powyższy wzór wprost, i najpierw mnożą s² razy (X’X)^-1 czyli skalar razy macierz która bywa 7 na 7 – to jest okropne marnotrawstwo wysiłku, przez s² wystarczy pomnożyć na końcu kiedy wynik jest 1 na 1.

Podobnie ma się rzecz z liczeniem c’(X’X)^-1c. W wektorze c występują często zera – nie wszystkie parametry wchodzą do badanej kombinacji liniowej. Rozważmy mnożenie c’(X’X)^-1c w 2 krokach: najpierw c’(X’X)^-1 = z’; potem z’c.

Wyliczając z’=c’(X’X)^-1:

1. nie bierzemy pod uwagę tych wierszy oraz (X’X)^-1 dla których w c występują zera (możemy je wykreślić)

2. nie musimy też wyliczać tych elementów z’ które odpowiadają zerom w c – bo wyliczając z’c i tak byśmy je pominęli; czyli wykreślamy sobie odpowiednie kolumny (X’X)^-1 (o tych samych numerach co numery wykreślonych wcześniej wierszy).

Potem wyliczone elementy wektora z mnożymy razy niezerowe elementy c, sumujemy i mamy c’(X’X)^-1c. Wystarczy to potem pomnożyć przez s², wziąć pierwiastek i mamy D(g^).

Jeśli ktoś lekkomyślnie i niepotrzebnie wyliczy całe V^(b^) i potem będzie mnożył dokładnie c’V^(b^)c to na sprawdzianie MUSI mu zabraknąć czasu i słusznie. Trzeba się uczyć optymalizować obliczenia – to jest bardzo ważne także przy konstrukcji pewnych rodzajów kodów komputerowych. J

MAŁY DODATEK DLA CHĘTNYCH (PONAD STANDARDOWY PROGRAM)

Oczywiście możemy dalej wykorzystać powyższą generalizację – nie tylko dla testu t, ale dla testu F. Ogólnie możemy testować p liniowych kombinacji parametrów regresji – i to niekoniecznie ich zerowanie (jak w Zajęciach 5) ale równość z dowolną stałą. Tak dochodzimy do najbardziej ogólnej wersji testu F – jej szczególnymi przypadkami są wszystkie poznane wcześniej testy.

Ogólna postać testu F: łączne testowanie p liniowych restrykcji na parametry regresji.

(ten test jest przedstawiony w wykładach powieszonych w pliku pdf: Fragmenty notatek wykładowych – tylko tam jest niekonsekwencja w notacji – tamtejsze c to tutaj d żeby nie było konfliktu z tym co powyżej) Ten test uogólnia dane powyżej rozumowanie – powyżej mogliśmy testować jedną kombinację liniową współczynników regresji g = c’b, teraz możemy testować ŁĄCZNE zachodzenie kilku takich równości: zamiast wektora c i skalara gamma weźmiemy macierz S (tworzy ją kilka wektorów c’ jeden pod drugim) i wektor d (tworzy go kilka odpowiednich wartości g). Wtedy będziemy testować:

H₀: Sb=d

H₁: Sb¹d

(S ma tyle kolumn, ile jest parametrów w b, a S i d mają tyle wierszy, ile kombinacji testujemy, czyli p) – wymiary to S (p´k); d (p´1)

(w H₀ mamy oczywiście koniunkcję a w H₁ alternatywę zaprzeczeń–jak to w teście F)

Statystyka testowa ma postać:

i przy prawdziwości H₀ rozkład F(p,T-k) – czyli testowanie wygląda tak, jak to omówiono w Zajęciach 5. Rozpatrywaliśmy tam test F łącznej istotności bloku współczynników regresji – odpowiada to przyjęciu w macierzy S bloku zer i bloku – macierzy jednostkowej S= [0 I] (oczywiście kiedy odpowiednio ułożymy kolejność parametrów – najpierw te, których nie testujemy, potem te, których zerowanie chcemy testować); natomiast wektor d to wektor zerowy (bo testujemy zerowanie). Załóżmy, że mamy parametry b‘ = [b₀ b₁ b₂ b₃ b₄] i chcemy testować łączne zerowanie b₂ , b₃ i b₄

Wtedy:

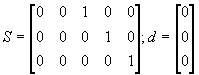
Układ Sb=d jest macierzowym zapisem następujących równości:

b₂ = 0 i b₃ = 0 i b₄ = 0.

Oczywiście za pomocą tak ogólnej wersji testu F możemy testować bardziej skomplikowane hipotezy – konstruując wiersze macierzy S zgodnie z tym, co wyżej napisano o wektorze c – czyli rozpatrując łączne testowanie kilku kombinacji liniowych parametrów.

Taki test ma bardzo interesujące zastosowanie. Przypomnijmy sobie z Zajęć 4 jak konstruowany był (1-alfa) procentowy przedział ufności dla pojedynczego parametru: to były te wszystkie wartości b_i* dla których na poziomie istotności alfa nie było podstaw do odrzucenia hipotezy H₀: b_i=b_i*. Oczywiście przedziały ufności były dla każdego parametru niezależnie (jak to w teście t). Teraz możemy sobie wyobrazić generalizację przedziału ufności – czyli OBSZAR UFNOŚCI. Dla p parametrów będzie to najmniejszy (w sensie „objętości”) podzbiór losowy R^p zawierający z ustalonym prawdopodobieństwem alfa wektor p nieznanych parametrów (b_i+1 ,..., b_i+p)’ a kiedy będziemy mieli konkretny obszar, to będzie :pojedyncza realizacja itd.

Dla przykładu możemy rozważyć dwa parametry. Można by pomyśleć, że dla wnioskowania o nich łącznie trzeba wziąć prostokąt – iloczyn kartezjański ich przedziałów ufności. Oczywiście to błąd – analogiczny do tego, że o łącznym zerowaniu 2 parametrów nie można wnioskować z wyniku 2 testów typu t. Można pokazać, że jeśli poszczególne przedziały mają ufność 1-a1 oraz 1-a2, to taki prostokąt jest obszarem o ufności co najmniej 1-a1-a2. Ale jest tu „co najmniej” i nie jest „najmniejszym”.

Wykorzystując powyższy test możemy stworzyć łączny obszar ufności, który będzie dla 2 parametrów pewną elipsą na płaszczyźnie. Trudno wyliczyć współrzędne tej elipsy, ale łatwiej można symulacyjnie wyznaczyć ją np. Excelem.

Taka elipsa – łączny obszar ufności – dostarcza nam informacji, jakich ŁĄCZNIE wartości nieznanych parametrów możemy oczekiwać. Jest to dużo bardziej dokładna informacja niż ta pochodząca ze standardowego przedziału ufności dla każdego parametru osobno.

Dany powyżej test F ma postać tak ogólną, że pozwala również na wyliczenie obszaru ufności dla liniowych kombinacji parametrów – przykładowo w modelu (3) powyżej, czyli:

ln y_t= a₀ + a₁ ln z_t + a₂ ln² z_t+a₃ ln v_t + a₄ ln² v_t + a₅ ln z_t ln v_t + e_t

gdzie elastyczność y_t po z_t jest dana wzorem:

El yt/zt = a₁ + 2 a₂ ln z_t + a₅ ln v_t

a elastyczność y_t po v_t jest dana wzorem:

El yt/vt = a₃ + 2 a₄ ln v_t + a₅ ln z_t

możemy zbudować łączny obszar ufności dla tych dwóch elastyczności – daje to nam lepszą orientację w tym, jakie kombinacje wartości elastyczności są „prawdopodobne” a jakie raczej nie.

Dla zbudowania obszaru ufności dla 2 parametrów regresji b_i oraz b_j macierz S będzie miała 2 wiersze z samymi zerami, tylko w pierwszym wierszu na i-tym miejscu a w drugim wierszu na j-tym miejscu będzie mieć jedynki – np.

0 0 1 0 0 0

0 0 0 1 0 0

odpowiadałoby w modelu powyżej badaniu parametrów a₂ oraz a₃ .

Jak zbudować obszar ufności dla 2 parametrów w Excelu?

Np. dla modelu

ln y_t= a₀ + a₁ ln z_t +a₂ ln v_t + e_t

i dla parametrów a₁ i a₂ – oczywiście trzeba mieć dane...

Trzeba w zrobić prostokątny obszar komórek, w którym wzdłuż jednej krawędzi (wiersza) będą wartości co np. 0,02 (zakres trochę większy niż przedział ufności dla jednego parametru); wzdłuż drugiej krawędzi (kolumny) wartości co 0,02 analogicznie tylko dla drugiego parametru (czyli np. 0,2 0,22 0,24 ) (skok może być co 0,01 lub 0,05 lub 0,1 itd. - zależy od skali parametrów); w środku tego wiersza (kolumny) będzie mniej więcej punkt odpowiadający ocenie MNK; w środku obszaru będzie punkt o współrzędnych będących ocenami MNK pary badanych parametrów.

Wnętrze takiego prostokąta chcemy wypełnić.. w każdej kratce chcemy mieć wynik testu F, że nasze współczynniki wynoszą dokładnie tyle, ile jest na skalach wzdłuż krawędzi (wiersza i kolumny).

Żeby to zrobić: macierz S będzie ustalona (będzie mieć bardzo prostą postać, jak powyżej). Wobec tego macierz w kwadratowym nawiasie ze wzoru statystyki testowej można sobie na boku RAZ wyliczyć i nazwać np. G. (tam jest sporo razy macierz.iloczyn) Wektor d musi się zmieniać, według tego co jest na krawędziach obszaru. W excelu to jest trudno zrobić. Ja zrobiłem tak:

Trzeba zrobić jeden wektor taki (0 1) a drugi taki (1 0) i nazwać je np. fa i fb (jak pomyśleć to są to wektory bazowe). Potem w formule robimy takiego łamańca (fa*S$15+fb*$R30) i to będzie d transponowane (przyjmuję, że S15 i R30 to komórki na skali; skala – wiersz jest w wierszu 15 (zadolarowana, żeby się dało rozciągać) skala – kolumna jest w kolumnie R, czyli wykres się zaczyna w R15, a właściwie w S16.

Oczywiście poziom istotności mamy gdzieś z boku nazwany alfa, a w innym miejscu z boku mamy Fkryt, czyli wartość krytyczną z testu F, oczywiście mamy gdzieś z boku policzone es kwadrat. Więc możemy zrobić tak, że w każdej komórce mamy wartość statystyki (odwołujemy się do zrobionej wcześniej macierzy G). Przypuśćmy, że ta formuła która wylicza wartość statystyki to Femp; więc zróbmy tak: Użyjemy funkcji JEŻELI (test; wartość jeżeli prawda; wartość jeżeli fałsz). I zrobimy tak: Jeżeli (Femp < Fkryt; 1 ; 0) czyli będziemy mieli 1 gdy nie ma podstaw do odrzucenia H0 a zero w przeciwnym wypadku. Jak się uda, to robimy F2 SHIFT+CTRL+ENTER, rozciągamy komórkę za prawy dolny róg na całość, i można na wszelki wypadek jeszcze raz F2 SHIFT+CTRL+ENTER.

Potem zaznaczamy całość razem ze skalą pionową i poziomą, klikamy wykres typ Powierzchniowy i podtyp pierwszy w drugim rzędzie.

Dobrze jest także zaznaczyć sobie (nawet na oko według skali) punkt ocen MNK oraz linie odpowiadające krańcom przedziałów ufności dla obydwu parametrów.

Mi się udało, wychodzi BARDZO ładnie i jest bardzo bardzo pouczające.

Rezultat może wyglądać np. tak:

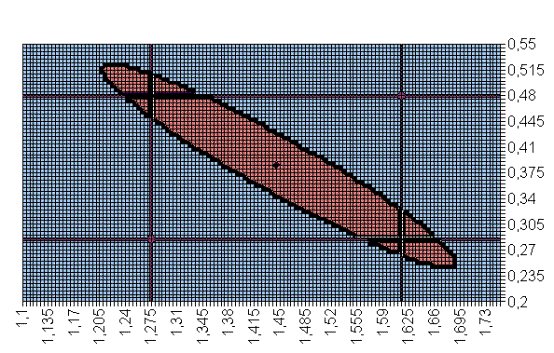
Na rysunku jest zaznaczony 95% obszar ufności dla 2 parametrów regresji oraz 95% przedziały ufności dla każdego z nich osobno – współrzędne punktu w środku to oceny MNK parametrów. Widać wyraźnie, że obszar ufności dostarcza jakościowo innej informacji o łącznym kształtowaniu się badanych parametrów niż rozpatrywanie iloczynu kartezjańskiego oddzielnych przedziałów ufności. Tu analiza obszaru ufności wyklucza (tzn. czyni „mało prawdopodobnymi”) pary wartości parametrów w północno – wschodnim i południowo – zachodnim narożniku – tzn. sytuacje, kiedy obie wartości są „małe” lub obie „duże”.

KONIEC MAŁEGO DODATKU DLA CHĘTNYCH (PONAD STANDARDOWY PROGRAM)

Podstawowe umiejętności konieczne do rozwiązywania zadań:

1. Zapisywanie wektora c dla wnioskowania o liniowej kombinacji parametrów (m.in. dla sumy parametrów, elastyczności lub wartości teoretycznej zmiennej objaśnianej).
2. Wyznaczanie błędu średniego szacunku liniowej kombinacji parametrów [D(g^)]
3. Wnioskowanie o liniowej kombinacji parametrów analogicznie jak o pojedynczym parametrze w Zajęciach 4.

Co najczęściej myli się w zadaniach?

Najczęściej trudno uświadomić sobie, jak „podciągnąć” postawiony w zadaniu problem pod schemat g = c’b; ponadto często występuje źle zrobiony wektor c <np. zawierający b> lub niepotrzebnie czasochłonne wyliczanie zbędnych wielkości (zagadnienia te opisano powyżej).

Zadanie Laboratoryjne

(Under Construction)

Ćwiczenia tablicowe:

(Under Construction)

Problem do przemyślenia na następne zajęcia:

(Under Construction)