Liniowe modele wielorównaniowe

notacja, klasyfikacja

Wstęp

W poprzednich zajęciach przedstawiliśmy problem regresji z losowymi zmiennymi objaśniającymi. Przypomnijmy dwa aspekty:

-w pewnych przypadkach sama konstrukcja modelu wymusza na nas rozważanie losowych zmiennych objaśniających

-konsekwencje losowości zmiennych objaśniających mogą być poważne (pokazaliśmy, że może to prowadzić nawet do niezgodności estymatora MNK w przypadku 2c – kiedy bieżące zmienne objaśniające są skorelowane z bieżącymi składnikami losowymi.)

Ważnym rodzajem modeli, w których natykamy się na problem losowych zmiennych objaśniających, są modele wielorównaniowe. Mają one ważną i użyteczną interpretację ekonomiczną, występują w nich interesujące problemy statystyczne. Model wielorównaniowy opisuje „równoczesne” kształtowanie się wartości kilku zmiennych „objaśnianych” – opisujemy w ten sposób system – kilka zmiennych potencjalnie powiązanych zależnościami. Ponieważ opisujemy zachowanie kilku zmiennych objaśnianych, musimy mieć tyle właśnie równań. Przez „równoczesne kształtowanie” rozumiemy, że te same zmienne mogą występować w kilku równaniach – raz po lewej a raz po prawej stronie. Układem równań opisujemy zależności między rozważanymi zmiennymi dla każdej obserwacji t. Na użytek modeli wielorównaniowych inaczej klasyfikujemy zmienne, dlatego też określenie „objaśniana” jest w cudzysłowie. Będziemy rozważać zmienne:

endogeniczne – takie, których wartości kształtują się wewnątrz rozważanego układu. Są to zmienne, które mają swoje własne równania opisujące ich powstawanie. Zmienne endogeniczne zwykle są losowe na mocy konstrukcji modelu – ich równania mają zwykle składniki losowe lub mają po prawej stronie inne zmienne endogeniczne.

egzogeniczne – takie, które kształtują się na zewnątrz (procesu ich powstawania nie modelujemy) i wchodzą do układu równań tylko poprzez obserwowane wartości – dla zmiennych egzogenicznych nie specyfikujemy równań pokazujących jak powstają. Zmienne egzogeniczne możemy traktować tak, jakby były nielosowe.

W niniejszych zajęciach będziemy rozważać następujące problemy:

notacja-pokażemy notację, która będzie w dalszym ciągu wykorzystywana (notacja w ekonometrii to podstawa, więc proszę się przyłożyć)

klasyfikacja-wykorzystując notację, rozważymy różne rodzaje modeli wielorównaniowych według tego, jakie problemy statystyczne w nich występują.

Tu ograniczamy się tylko do liniowych zależności między zmiennymi. Przykładowy model to:, ogólnie mamy m równań.

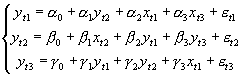, t = 1,2,...,T

mamy w modelu składniki losowe: , układamy je w wektor – wiersz e_t. To różnica w porównaniu z modelami jednorównaniowymi (jak KMRL), gdzie e_t był skalarem.

o parametrach zakładamy, że nie mogą zachodzić związki między parametrami różnych równań. Np. wykluczamy możliwość, że b₁ = a₁ – coś takiego mogłoby wynikać z np. teorii ekonomicznej. To WYKLUCZAMY.

o składnikach losowych:

-standardowo zakładamy, że mają zerową wartość oczekiwaną:

1.

w naszym przykładzie:

-o wariancjach i kowariancjach pomiędzy składnikami losowymi:

Ø o kowariancjach pomiędzy składnikami losowymi RÓŻNYCH RÓWNAŃ, TEJ SAMEJ OBSERWACJI.

Kowariancje pomiędzy składnikami losowymi różnych równań dla tego samego t (indeksu obserwacji) są zebrane w tzw. macierzy równoczesnych kowariancji składników losowych oznaczonej jako V(e_t):

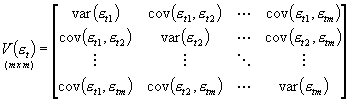
2. oraz

założenie, że oznacza, że macierz równoczesnych kowariancji nie zależy od t – jest taka sama dla każdej obserwacji (bo NIE zakładamy, że ). Wobec tego, wszystkie wariancje składników losowych są STAŁE, a kowariancje pomiędzy składnikami losowymi różnych równań są takie same dla każdej obserwacji. Zakładamy, że ta macierz jest nieosobliwa. Każda macierz kowariancji musi być kwadratowa, symetryczna i nieujemnie określona, a ponieważ dodatkowo zakładamy, że jest nieosobliwa, to w sumie jest dodatnio określona. Jeśli mamy do czynienia z przypadkiem, że macierz równoczesnych kowariancji jest diagonalna (macierz diagonalna to taka, że wszystkie elementy poza główną przekątną są zerowe), to oznacza, że składniki losowe różnych równań dla tej samej obserwacji są nieskorelowane.

Ø o kowariancjach pomiędzy składnikami losowymi DLA RÓŻNYCH OBSERWACJI:

3.

Zakładamy tu, że wszystkie składniki losowe dla różnych obserwacji są nieskorelowane. Np. jeśli modelujemy gospodarkę w kolejnych latach i mamy równania konsumpcji oraz inwestycji, to zakładamy, że zakłócenie równania inwestycji w danym roku jest niezależne od zakłóceń tego samego równania w innych latach oraz zakłóceń innych równań w innych latach.

Rozważmy układ m równań opisujących kształtowanie się wartości m zmiennych endogenicznych. Możemy taki układ zapisać „rozpisując” dokładnie każde równanie, lub stosując notację macierzową. Na mocy konwencji po lewej stronie zapisujemy wartości zmiennych endogenicznych. Przykładowo:

(1) ln v_t= a₀ + a₁ ln z_t + a₂ k_t + h_t + u_t1

ln z_t= b₀ + b₁ ln v_t-1 + b₂ g_t + u_t2

Liczba równań m = 2

Tutaj zmienne endogeniczne to:

ln v, ln z

Zmienne egzogeniczne to:

g, h, k

Zauważmy, że w modelu występuje opóźniona zmienna endogeniczna ln v_t-1

u_t1 u_t2

to składniki losowe poszczególnych równań.

Na użytek modelowania wielorównaniowego klasyfikujemy zmienne w jeszcze jeden sposób, mianowicie na łącznie współzależne i z góry ustalone .

Zmienne łącznie współzależne to bieżące zmienne endogeniczne (czyli bez opóźnień). Wektor zmiennych łącznie współzależnych (wektor-wiersz) oznaczamy y_t. W naszym przykładzie:

y_t = ( ln v_t ln z_t )

Zauważmy, że wektor y ma zawsze m elementów – tyle, ile jest równań, bo każda bieżąca wartość zmiennej endogenicznej ma swoje równanie.

Zmienne z góry ustalone to: opóźnione zmienne endogeniczne, zmienne egzogeniczne i zmienne sztuczne (takie jak 1-ka przy wyrazach wolnych). Wektor zmiennych z góry ustalonych oznaczamy x_t. W naszym przykładzie:

x_t = ( ln v_t-1 k_t h_t g_t 1)

liczbę zmiennych z góry ustalonych (czyli kolumn x_t) oznaczmy przez k.

Podobnie możemy zgrupować w wektorze składniki losowe równań:

e_t = (u_t1 u_t2)

wektor e_t ma taki sam wymiar jak y_t – czyli m na 1.

Układ równań (1) to przykład zapisu POSTACI STRUKTURALNEJ modelu wielorównaniowego. Postać kolejnych równań wynika z postulowanych przez badacza zależności między zmiennymi; parametry postaci strukturalnej mają interpretację. Równania postaci strukturalnej to np. funkcja konsumpcji, funkcja inwestycji itd. Ogólnie jest to odzwierciedlenie pewnej struktury zależności ekonomicznych. Postać strukturalna związana jest z konstrukcją i interpretacją ekonomiczną modelu. W odróżnieniu od niej będziemy rozpatrywać POSTAĆ ZREDUKOWANĄ – będzie ona miała istotne znaczenie w kontekście estymacji.

Postać strukturalną można zapisać „klamerkowo” – równanie po równaniu – jak w (1). Dla modelu liniowego można także rozważyć przedstawienie jej w postaci macierzowej. Wykorzystamy do tego zdefiniowane powyżej wektory y_t i x_t. Rozważmy zapis:

(2)

dla pojedynczej obserwacji o numerze t, lub łącznie dla wszystkich T obserwacji:

Y to wektory y_t ułożone jeden pod drugim, od y₁ do y_T

X to wektory x_t ułożone jeden pod drugim, od x₁ do x_T

Aby zachowane były wymogi mnożenia i sumowania macierzy [patrz wymiary x_t, y_t i e_t] , B musi być macierzą kwadratową m na m, a G macierzą k na m. Zauważmy, że w zapisie (2) wszystko jest po lewej stronie znaku równości, a po prawej pozostają tylko składniki losowe. Trzeba tylko ustalić postać macierzy B i G - musimy w nich rozmieścić parametry postaci (1). Robimy to, pamiętając że:

kolumny macierzy B i G (jest ich m) odpowiadają równaniom postaci klamerkowej (parametry 1-go równania będą w 1 kolumnie B i G)

wiersze macierzy B i G odpowiadają kolejnym elementom odpowiednio y_t i x_t.

[czyli w i-tej kolumnie i j-tym wierszu G będzie parametr, który występuje w i-tym równaniu przy zmiennej, która jest na j-tym miejscu w wektorze x_t.

na mocy konwencji i-ta zmienna endogeniczna w wektorze y_t jest objaśniana (po lewej stronie) w i-tym równaniu

[to znaczy, że i-ty y jest objaśniany (czyli już po lewej stronie, z parametrem 1) w i-tym równaniu. Czyli w macierzy B w i-tym wierszu i i-tej kolumnie [więc na przekątnej] będą jedynki.]

ponieważ wszystkie parametry i zmienne przenosimy na lewą stronę, trzeba pozmieniać znaki parametrów.

Jeśli dana zmienna nie występuje w i-tym równaniu – wstawiamy do macierzy 0, jeśli występuje bez parametru – wstawiamy jedynkę.

Czyli wypełniając macierze B i G idziemy kolumnami (czyli rówaniami) i w każdej kolumnie idziemy wzdłuż y_t i potem x_t i patrzymy, czy w danym równaniu jest zmienna, i z jakim parametrem. Możemy sobie dla ułatwienia opisać kolumny – zmiennymi objaśnianymi lub numerem równania, i wiersze – elementami y_t (w B) i elementami x_t (w G) - trzeba pilnować kolejności!

W naszym przykładzie macierze B i G będą miały postać:

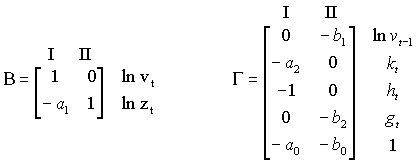
znaków nie zmieniamy tylko przy jedynkach w macierzy B bo zmienne objaśniane już są po lewej stronie.

Czyli ostatecznie układ (1) w zapisie macierzowym ma postać:

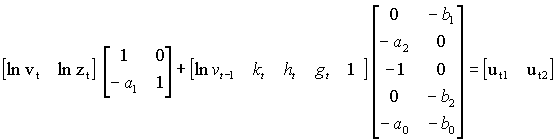
Są to po prostu dwa zapisy („klamerkowy” <bo równania zwykle łączy się klamrą> i macierzowy) postaci strukturalnej modelu wielorównaniowego. Żeby model zapisać w postaci macierzowej, trzeba prawidłowo sklasyfikować zmienne – czyli wyznaczyć wektory y_t i x_t a następnie wypełnić macierze B i G parametrami z postaci „klamerkowej”, zerami i jedynkami.