Zajęcia 16

Analiza dynamicznego modelu wielorównaniowego na przykładzie modelu Kleina

1. Postać zredukowana z restrykcjami.

Rozważamy model w postaci zredukowanej z restrykcjami. Załóżmy, że mamy zgodne oceny nieznanych parametrów strukturalnych modelu. W miejsce nieznanych elementów macierzy B i G wstawiamy ich oceny (uzyskujemy B^ i G^); wtedy możemy otrzymać:

[ten wzór musimy zastosować dla modelu niejednoznacznie identyfikowalnego. W modelu jednoznacznie identyfikowalnym postać zredukowana z restrykcjami jest tożsama z postacią zredukowaną bez restrykcji (bo nie ma restrykcji), wtedy ]

Oszacowana postać zredukowana z restrykcjami to:

(1)

co można zapisać jako:

(2)

gdzie y_t-1 to wektor wartości WSZYSTKICH opóźnionych (o 1 okres) zmiennych endogenicznych, z_t to wektor bieżących wartości zmiennych egzogenicznych. Wektor x_t wartości zmiennych z góry ustalonych dzielimy tu na wyraz wolny (odpowiada mu 1-ka przy wektorze d₀ której nie zapisujemy), opóźnienia zmiennych endogenicznych (w y_t-1) oraz zmienne egzogeniczne (w wektorze z_t). Odpowiednio do tego wiersze macierzy P^^ rozmieszczamy między macierze d₀^ D₁^ i D₂^. Należy pamiętać, że macierz D₁^ jest kwadratowa – wypełniamy elementami P^^ tylko te jej wiersze, które odpowiadają opóźnieniom zmiennych endogenicznych rzeczywiście występującym w modelu – pozostałe wiersze zawierają zera (WAŻNE: kolejność wierszy w D₁^ wynika z kolejności zmiennych w y_t-1 która musi być taka sama jak w y_t !!!).

W takim modelu bieżące wartości zmiennych egzogenicznych mają wpływ na bieżące wartości zmiennych endogenicznych, które z kolei poprzez człon: ...+ y_t-1D₁+ mają wpływ na przyszłe wartości zmiennych endogenicznych. Gdy macierz D₁ nie jest macierzą zerową (czyli gdy w modelu występują opóźnione zmienne endogeniczne) mamy do czynienia z modelem dynamicznym – bieżące wartości zmiennych endogenicznych zależą od całej przeszłości zmiennych egzogenicznych. Ponieważ to macierz D₁ odpowiada za transmisję wpływu z okresu na okres – to od jej własności będą zależeć własności dynamiczne całego modelu.

Przykład: Dla modelu Kleina:

B^=

	C	I	Wp	X	P	K
C	1	0	0	-1	0	0
I	0	1	0	-1	0	-1
Wp	-0,81018	0	1	0	1	0
X	0	0	-0,43886	1	-1	0
P	-0,0173	-0,15022	0	0	1	0
K	0	0	0	0	0	1

G^=

	C	I	Wp	X	P	K
P-1	-0,21623	-0,61594	0	0	0	0
X-1	0	0	-0,14667	0	0	0
K-1	0	0,157788	0	0	0	-1
Wg	-0,81018	0	0	0	0	0
G	0	0	0	-1	0	0
T	0	0	0	0	1	0
A	0	0	-0,1304	0	0	0
1	-16,5548	-20,2782	250,2938	0	0	0

P^^=

	C	I	Wp	X	P	K
P-1	0,768457	0,743385	0,663486	1,511842	0,848357	0,743385
X-1	0,178845	-0,0076	0,221827	0,171247	-0,05058	-0,0076
K-1	-0,10471	-0,18195	-0,1258	-0,28666	-0,16086	0,818048
Wg	1,34781	0,124073	0,645949	1,471884	0,825934	0,124073
G	0,663588	0,153142	0,797289	1,81673	1,019442	0,153142
T	-0,12847	-0,17588	-0,13357	-0,30435	-1,17078	-0,17588
A	0,158997	-0,00675	0,197208	0,152242	-0,04497	-0,00675
1	-264,197	38,885	-349,174	-225,312	123,8621	38,885

Więc:

d₀^=

-264,197

38,885

-349,174

-225,312

123,8621

38,885

D₂^=

	C	I	Wp	X	P	K
Wg	1,34781	0,124073	0,645949	1,471884	0,825934	0,124073
G	0,663588	0,153142	0,797289	1,81673	1,019442	0,153142
T	-0,12847	-0,17588	-0,13357	-0,30435	-1,17078	-0,17588
A	0,158997	-0,00675	0,197208	0,152242	-0,04497	-0,00675

D₁^=

	C	I	Wp	X	P	K
C-1	0	0	0	0	0	0
I-1	0	0	0	0	0	0
Wp-1	0	0	0	0	0	0
X-1	0,178845	-0,0076	0,221827	0,171247	-0,05058	-0,0076
P-1	0,768457	0,743385	0,663486	1,511842	0,848357	0,743385
K-1	-0,10471	-0,18195	-0,1258	-0,28666	-0,16086	0,818048

2. Równowaga długookresowa.

Rozważmy następujące zagadnienie:

Przypuśćmy, że znajdujemy się w chwili umownie oznaczonej jako t = 0. Bieżące wartości zmiennych łącznie współzależnych to y₀; bieżące wartości zmiennych egzogenicznych to z₀. Zaniedbajmy składniki losowe – ale tylko na użytek wyprowadzeń. (na egzaminie proszę ich NIE zaniedbywać – tutaj po prostu interesujemy się przede wszystkim deterministyczną stroną równania).

Załóżmy, że w całej przyszłości wartości zmiennych egzogenicznych nie zmienią się i pozostaną na pewnym poziomie równowagi ; gdzie = z₀ = z₁ = z₂ = z₃..... Jak w miarę upływu czasu będą kształtować się wartości zmiennych endogenicznych? Na mocy równania:

itd.

podstawiając w dalszym ciągu za y_t-1 możemy pokazać, że bieżąca wartość zmiennych egzogenicznych (y_t) będzie zależeć tylko od warunku początkowego y₀ oraz od poziomu równowagi zmiennych egzogenicznych :

(3) .

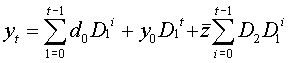[zakładamy, że macierz podniesiona do potęgi zerowej to macierz jednostkowa; zaś potęgowanie macierzy to mnożenie kolejno przez nią samą] Widzimy, że kształtowanie się wartości y_t dla dużego t będzie zależeć od tego, co się dzieje z macierzą D₁ podniesioną do wysokiej potęgi. Jeśli macierz D₁^t dąży do macierzy zerowej dla t ® ¥, wtedy odpowiednie sumy zastępujemy przez ich granice, natomiast składnik y₀D₁^t zeruje się:

(4) ,

[ostatnia równość definiuje „y w stanie równowagi przy pod warunkiem (w funkcji) wartości z w stanie równowagi”] Przy ustalonych wartościach zmiennych egzogenicznych system „powraca do równowagi” wychodząc od dowolnych wartości y₀ – co można inaczej opisać mówiąc, że warunek początkowy y₀ nie ma wpływu na punkt równowagi długookresowej. Możemy wartości y₀ rozpatrywać jako pewne zaburzenie wartości zmiennych endogenicznych w równowadze ; wtedy widzimy, że zaburzony system powraca do stanu równowagi „zapominając” z czasem o jednorazowym zakłóceniu.

Przykład: równowaga w modelu Kleina.

Jeżeli w modelu Kleina ustalimy zmienne egzogeniczne na poziomie odpowiadającym obserwacji 1941, czyli przyjmiemy:

	Wg	G	T	A
=	8,5	13,8	11,6	1941

oraz początkowe wartości zmiennych endogenicznych na poziomie obserwacji 1941 czyli przyjmiemy:

	C	I	Wp	X	P	K
y0 =	69,7	4,9	53,3	88,4	23,5	209,4

To dążenie zmiennych egzogenicznych do równowagi długookresowej przedstawiają poniższe wykresy:

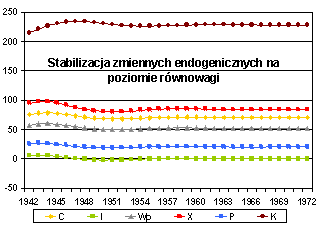
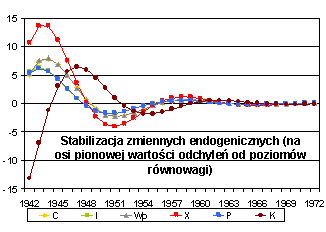
Rys. 1: Równowaga długookresowa w modelu Kleina:
A: (poziomy zmiennych)	B: (odchylenia od poziomów równowagi)

Powyższe rysunki sugerują stabilność modelu Kleina – widać (Rys. A) jak zmienne endogeniczne ustalają się na poziomie równowagi.

Przy danych powyżej warunkach poziomy równowagi zmiennych endogenicznych wynoszą odpowiednio:

	C	I	Wp	X	P	K
=	70,49993	8,89289E-15	52,16463	84,29993	20,53529	228,2285

Tutaj popełniamy pewną niekonsekwencję – de facto zmienna A jest liniowym trendem deterministycznym, który zakładamy w okresie obejmującym próbę, w którym szacujemy parametry. Jeśli trend ten „działa” dalej, to oczywiście z upływem ‘czasu’ zmienna endogeniczna W_P będzie rosnąć (lub maleć) do nieskończoności, a z nią wszystkie inne zmienne endogeniczne. Tutaj zakładamy (dość niekonsekwentnie) że A to pewna zmienna egzogeniczna (jak inne), która najpierw (w próbie) sobie rosła, a potem (w kolejnych, rozważanych powyżej) okresach ustabilizowała się. To dość dowolne postępowanie, ale robimy to tylko dla ilustracji – żeby pokazać coś takiego jak poziomy równowagi długookresowej. Poważniejsze i bardziej sensowne potraktowanie trendu w modelu Kleina byłoby bardziej skomplikowane). Tutaj więc dla uproszczenia postępujemy nie do końca poprawnie.

3. Badanie stabilność modelu.

Powyżej założyliśmy, że D₁^t dąży do macierzy zerowej dla t ® ¥. Warunek ten jest zwany „warunkiem stabilności modelu”. Można pokazać, że jego spełnienie jest związane z tzw. wartościami własnymi macierzy D₁. Stabilność modelu zapewnia wymaganie, aby wszystkie wartości własne macierzy D₁ były co do modułu mniejsze od jedności. Macierz D₁ zwykle nie jest macierzą symetryczną, więc jej wartości własne mogą być zespolone. Wartości własne kwadratowej macierzy A to pierwiastki (miejsca zerowe) jej równania charakterystycznego:

det(A-lI) = 0

(l to skalar – zmienna w tym równaniu, det() oznacza wyznacznik macierzy, macierz jednostkowa jest takiego stopnia by odejmowanie było zdefiniowane, dalej l pełni rolę niewiadomej, jakby x w równaniu).

Macierz D₁ zwykle zawiera zerowe wiersze (odpowiadające tym zmiennym endogenicznym których opóźnienia NIE występują w modelu); dla takiej macierzy możemy skorzystać ze wzoru na wyznacznik macierzy w podziale na bloki z blokami zerowymi:

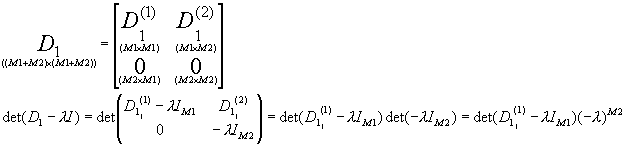
Więc równanie charakterystyczne macierzy D₁:

ma M2-krotny zerowy pierwiastek; niezerowe pierwiastki charakterystyczne D₁ są tożsame z pierwiastkami D₁⁽¹⁾. W macierzy D₁ kolejność wierszy jest ściśle związana z kolejnością kolumn (w obydwu wypadkach musi być taka jak zmiennych w wektorze y), przekształcenie macierzy D₁ do postaci danej powyżej – z zerowymi wierszami „od końca” wymaga odpowiedniej zmiany kolejności kolumn!!!. W macierzy D₁ będą więc współczynniki z równań (kolumn P) odpowiadających tym zmiennym endogenicznym, których opóźnienia występują w modelu; i z tych wierszy P, które odpowiadają ich opóźnieniom.

Dla badania stabilności wystarczy więc rozważyć pierwiastki równania:

gdzie D₁⁽¹⁾ to niezerowa kwadratowa podmacierz D₁ odpowiadająca tym samym zmiennym w wierszu (opóźnionym) i kolumnie (w sensie zmiennej objaśnianej danego równania, bo kolumny odpowiadają równaniom)

Przykład: Dla modelu Kleina:

(tu pomijam daszki przy D₁)

Z oszacowania macierzy D₁ danego powyżej wybieramy odpowiednią podmacierz odpowiadającą D⁽¹⁾₁:

	X	P	K
X-1	0,171247	-0,05058	-0,0076
P-1	1,511842	0,848357	0,743385
K-1	-0,28666	-0,16086	0,818048

D₁⁽¹⁾ -lI =

0,171247-l	-0,05058	-0,0076
1,511842	0,848357-l	0,743385
-0,28666	-0,16086	0,818048-l

det(D₁⁽¹⁾-lI) = (0,171247-l)*(0,848357-l)*(0,818048-l)+1,511842*-0,16086*-0,0076+ - 0,28666*-0,05058*0,743385 +

- - 0,0076*(0,848357-l)*-0,28666 - 0,743385 * -0,16086*(0,171247-l) – (0,818048-l)*-0,05058*1,511842 chyba...

to by trzeba rozpisać dalej i wyliczyć pierwiastki J - pewnie będzie jeden rzeczywisty i para zespolonych.

Pierwiastki charakterystyczne wychodzą: (policzyłem sobie przy pomocy dodatku - patrz niżej) [w zadaniach podmacierz D₁ będzie max. 2 na 2 więc równanie będzie co najwyżej kwadratowe]

rzeczywisty:

l₁^ = 0.29730406

i zespolone:

l₂^ = 0.77017397 + 0.34944989i

l₃^ = 0.77017397 - 0.34944989i

moduł pierwiastka rzeczywistego (wartość bezwzględna) jest równy 0.29730406, więc <1,

moduł zespolonych (taki sam dla obydwu oczywiście) (a^2 + b^2)^0,5 = 0.84574415 czyli też < 1.

Wszystkie wartości własne D₁^ są co do modułu mniejsze od 1, więc model uznajemy za stabilny

[taka mała uwaga: w praktyce rozważamy tu OCENY PUNKTOWE D₁, więc mamy też oceny punktowe jej wartości własnych. Porządne badanie stabilności wymagałoby testowania hipotez dotyczących wartości własnych – a przynajmniej podania ich oceny ORAZ błędu średniego szacunku.

jest to dość skomplikowane, bo wartości własne są skomplikowanymi funkcjami parametrów postaci zredukowanej, ale daje się badać. Dla nas praktyczny skutek jest taki, że zbadanie stabilności wyłącznie na podstawie ocen punktowych traktujemy jako bardzo przybliżone, niedokładne]

W tych zajęciach – jak to zaznaczono – prowadzimy bardzo uproszczoną analizę, bo wcale nie uwzględniamy:

-elementów stochastycznych modelu („przyszłych epsilonów”)

-błędu estymacji parametrów

te elementy wprowadzają do naszego rozumowania niepewność, która w „porządnej” analizie powinna być dokładnie zbadana i oszacowana. Nie podejmujemy tego problemu, bo mamy miejsce tylko „wstęp do wstępu do” analizy dynamicznej.

DODATEK!! (żeby nie było że nie daję Państwu narzędzi tylko wymagam liczenia wartości własnych sposobem mnichów wczesnośredniowiecznych którzy jak wiadomo wartości własne macierzy asymetrycznych wyliczali na liczydłach). J

Pod linkiem http://digilander.libero.it/foxes/SoftwareDownload.htm mają Państwo freeware’owe pakiety dodatków matematycznych do Excela. Polecam dodatek: MATRIX 1.x - Matrix and Linear Algebra functions for EXCELâ

Trzeba go załadować (ok. 600 KB) rozpakować gdziekolwiek, potem w Excelu wejść w Narzędzia->dodatki->przeglądaj i skierować go do pliku matrix.xla

W excelu pojawią się Państwu dodatkowe funkcje baardzo przydatne, a w szczególności:

MatEigenvalue_QR(...).

Która zwraca wartości własne kwadratowej macierzy. UWAGA! Rezultat jest macierzą o 2 kolumnach i tylu wierszach ile wartości własnych, czyli ile wynosi stopień macierzy. Kolumny są dwie, bo wartości własne mogą byś zespolone i podawane są w postaci par liczb (a, b) zgodnie z notacją z = a + bi gdzie i to jednostka urojona. Więc moduł wyliczamy zgodnie ze wzorem powyżej i wszystko jest jak na talerzu. Mogą sobie więc Państwo to zainstalować (powinno jeszcze się przydać) i używać do badania stabilności.

Przy okazji: wielkie dzięki dla autorów pakietu, czyli Foxes Team jak rozumiem.

Wyliczanie wartości własnych wykorzystuje procedury iteracyjne więc nie jest super-dokładne – mogą Państwo otrzymać wartość własną rzędu E-16 zamiast zerowej..

4. Analiza mnożnikowa.

Na rys. 1 mamy przykład trajektorii zmiennych egzogenicznych „powracających” po „zaburzeniu” y₀ do stanu równowagi – oczywiście przy ustalonych odpowiednio zmiennych egzogenicznych na poziomie (jak powyżej opisano). Zastanówmy się, jak zmieniłyby się te przebiegi, gdyby wartość którejś zmiennej egzogenicznej została zaburzona.

A) Gdyby wartość jednej ze zmiennych egzogenicznych doznała w przeszłości (w okresie 0) jednorazowej zmiany („szoku”) – przełożyłoby się to zgodnie z (2) – na przyszłe wartości y_t wyłącznie przez zmienione wartości y w okresie 0. Spodziewamy się więc, że byłoby to równoznaczne ze zmianą wektora y₀ – więc nie zmieniłyby się wartości y w równowadze, zmieniłaby się wyłącznie ścieżka dotarcia do nich – czyli przebieg kolejnych wartości y_t w drodze do .

B) Gdyby wartość którejś zmiennej egzogenicznej została trwale zmieniona – oznacza to zmianę wartości wektora a więc i zmianę wartości równowagi .

Jaka jest różnica między przebiegami podstawowej trajektorii zmiennej w porównaniu z przypadkami A) oraz B)?

Zapiszmy równanie (3) dla różnych wartości z_t (tutaj znowu zaniedbujemy składniki losowe):

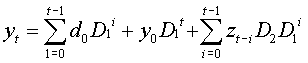
A)

W ostatniej sumie po prawej stronie występuje z_i dla i = 1,2,..,t – więc nie występuje z₀ – wartości z₀ oddziałują wyłącznie poprzez y₀.

po podstawieniu widzimy, że zmiana z₀ będzie oddziaływać na y_t poprzez składnik z₀D₂D₁^t. – więc jednostkowa i jednorazowa zmiana wartości zmiennej egzogenicznej r okresów temu (i tylko wtedy, przy ustalonych wartościach pozostałych zmiennych egzogenicznych) zmienia bieżącą wartość zmiennych endogenicznych y_t o D₂D₁^r jednostek.

Oczywiście D₂D₁^r to cała macierz z której wybieramy sobie odpowiednie wartości. Jest to macierz

mnożników pośrednich rzędu r:

(w tym wzorze przyda się Państwu podnoszenie macierzy do potęgi – w Matrix funkcja m_pow(macierz; potęga) )

B)

Z równania powyżej możemy również odczytać wpływ trwałej (podtrzymanej od okresu 0) jednostkowej zmiany wartości z_t na bieżące wartości zmiennych egzogenicznych: odzwierciedla go macierz mnożników skumulowanych rzędu r:

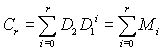
obrazują one wpływ jednostkowej zmiany wartości pewnej zmiennej egzogenicznej r okresów temu i w okresach kolejnych (przy ustalonych wartościach pozostałych zmiennych) na bieżące wartości zmiennych endogenicznych y_t.

Możemy rozważać co by się stało, gdyby podtrzymana zmiana z_t była trwała (w całej nieskończonej przeszłości) – odpowiada to zmianie i wobec tego również - zgodnie z równaniem (4) o D₂ (I-D₁)^-1. Jest to granica C_r dla r ® ¥ (która istnieje jeśli model jest stabilny). Otrzymujemy w ten sposób mnożnik całkowity:

którego wartości możemy interpretować jako odzwierciedlające wpływ jednostkowej zmiany wartości pewnej zmiennej egzogenicznej w całej przeszłości (przy ustalonych wartościach pozostałych zmiennych) na bieżącą wartość y_t [lub jeśli nam to potrzebne: na wartość y w równowadze długookresowej czyli ].

UWAGA: KIEDY ZMIENNE W MODELU SĄ W POSTACI LOGARYTMÓW WIELKOŚCI EKONOMICZNYCH, INTERPRETACJĘ W JEDNOSTKACH W ODNIESIENIU DO ZMIENNYCH ZASTĘPUJEMY INTERPRETACJĄ PROCENTOWĄ W ODNIESIENIU DO WIELKOŚCI EKONOMICZNYCH. (przykład poniżej przy M₂)

zasada interpretacji jest taka sama jak w przypadku parametrów modelu liniowego – patrz zajęcia 3 pod koniec.

Elementy macierzy mnożników odpowiadają tym zmiennym co elementy macierzy D₂ (która jest mnożnikiem bezpośrednim M₀, wszystkie macierze mnożników „dziedziczą” strukturę po D₂), mamy tylko przesunięcie w czasie o rząd mnożnika w odniesieniu do zmiennych egzogenicznych.

Dla przykładu w modelu Kleina M₂^ ma wartość:

Ct	It	Wpt	Xt	Pt	Kt
0,654196	0,311419	0,638671	0,965614	0,326943	1,01572	Wgt-2
0,807467	0,384381	0,788305	1,191848	0,403543	1,253693	Gt-2
-0,94061	-0,50831	-0,89574	-1,44891	-0,55318	-1,52021	Tt-2
-0,03735	-0,02567	-0,03352	-0,06302	-0,0295	-0,06578	At-2

(element wytłuszczony możemy interpretować tak:

Wzrost wartości zmiennej T (podatki i cośtam) o jedną jednostkę dwa okresy temu i tylko wtedy, przy ustalonych wartościach pozostałych zmiennych egzogenicznych, spowoduje spadek bieżącej wartości zmiennej Wp (płac w sektorze prywatnym) o około 0,89 jednostki.

możemy oczywiście interpretować dalej inne elementy w danym wierszu:

... oraz spadek bieżącej wartości zmiennej I (inwestycje netto) o około 0,51 jednostki a także....

UWAGA:

-warto wypisać, jakie są te „pozostałe zmienne egzogeniczne”, czyli napisać „przy ustalonych wartościach płac w sektorze budżetowym”etc.

-zamiast oznaczeń „wartość zmiennej I” warto używać nazw „wielkość inwestycji netto”

-a także używać konkretnych nazw jednostek – jeśli zmienna jest mierzona w milionach złotych piszemy: „spadek o około 510 tys.” )

jeśli interesuje nas wpływ łącznej zmiany kilku zmiennych, możemy w przybliżeniu zsumować odpowiednie elementy w wybranej kolumnie. Przykładowo, łączna interpretacja elementów zaznaczonych kursywą [2 i 3 element w 2 kolumnie] brzmi:

Równoczesny wzrost wartości zmiennych G (wydatków rządowych) oraz T (podatków) o jedną jednostkę dwa okresy temu i tylko wtedy, przy ustalonych wartościach pozostałych zmiennych egzogenicznych, spowoduje spadek bieżącej wartości zmiennej I (wielkość inwestycji netto) o około 0,13 jednostki. [0,38 – 0,51 = – 0,13]

Gdyby zmienne były logarytmami wielkości ekonomicznych, wtedy przykładowa interpretacja elementu równego –0,89 przy zmiennej endogenicznej ln P_t i egzogenicznej ln M_t mnożnika M₂ byłaby taka:

Wzrost wartości zmiennej M o jeden procent dwa okresy temu i tylko wtedy, przy ustalonych wartościach pozostałych zmiennych egzogenicznych, spowoduje spadek bieżącej wartości zmiennej P o około 0,89 procenta.

C₂^ ma postać:

Ct	It	Wpt	Xt	Pt	Kt
2,8869493	1,015720409	2,143511	3,90267	1,759159	1,844095	Wgt	Wgt-1	Wgt-2
2,5633313	1,253693043	2,645713	4,817024	2,171311	2,276147	Gt	Gt-1	Gt-2
-2,004787	-1,520210348	-1,851484	-3,524998	-2,673513	-2,707992	Tt	Tt-1	Tt-2
0,1150301	-0,065783311	0,168475	0,049247	-0,119228	-0,112648	At	At-1	At-2

(element wytłuszczony możemy interpretować tak:

Wzrost wartości zmiennej G (wydatki rządowe z pominięciem płac) o jedną jednostkę dwa okresy temu i w kolejnych okresach, przy ustalonych wartościach pozostałych zmiennych egzogenicznych, spowoduje wzrost bieżącej wartości zmiennej K (zasobu kapitału) o około 2.27 jednostki.

Ocena mnożnika całkowitego C_¥^ ma postać:

	Ct	It	Wpt	Xt	Pt	Kt
Wg	1,889338	0	1,10627	1,889338	0,783068	3,802326
G	1,3319901	0	1,365457	2,33199	0,966533	4,693171
T	-0,544604	0	-0,318884	-0,544604	-1,225721	-5,9517
A	0,1753475	0	0,233067	0,175347	-0,05772	-0,280269

(element wytłuszczony możemy interpretować tak:

Wzrost wartości zmiennej T (wielkość podatków pośrednich) o jedną jednostkę w całej przeszłości, przy ustalonych wartościach pozostałych zmiennych egzogenicznych, spowoduje spadek bieżącej wartości zmiennej X (dochodu narodowego) o około 0,54 jednostki.

Zera w kolumnie odpowiadającej inwestycjom możemy interpretować następująco – w równowadze zasób kapitału stały, więc występują jedynie inwestycje odtworzeniowe, inwestycje netto są więc równe zeru – co przy stałości K wynika z ostatniego równania modelu Kleina.

W powyższych interpretacjach wyłącznie na mocy konwencji przyczynę umieszczamy w przeszłości (r okresów temu), zaś skutek w okresie bieżącym. Oczywiście to nie jest istotne, ważne jest, by odstęp między przyczyną a skutkiem wynosił r okresów (tyle, ile wynosi rząd mnożnika). Możemy więc mieć przyczynę w okresie bieżącym a skutek po r okresach etc.

Pamiętajmy, że mnożniki podają tylko ODCHYLENIA w porównaniu z przebiegiem „w sytuacji bez szoku” badanych zmiennych endogenicznych. Analizując mnożniki możemy dociekać, jaka byłaby alternatywna ścieżka rozwoju danej zmiennej endogenicznej gdyby zamiast stałości wszystkich zmiennych egzogenicznych jedna z nich została (trwale lub impulsowo) zaburzona. Rozważmy dla przykładu następujący rysunek:

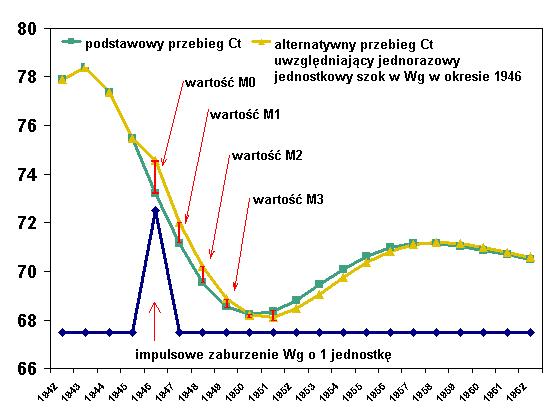
Rysunek 2. Wpływ zaburzeń Wg na wartości C

A. Wpływ jednorazowego jednostkowego szoku w Wg okresie 1946 na wartość C.

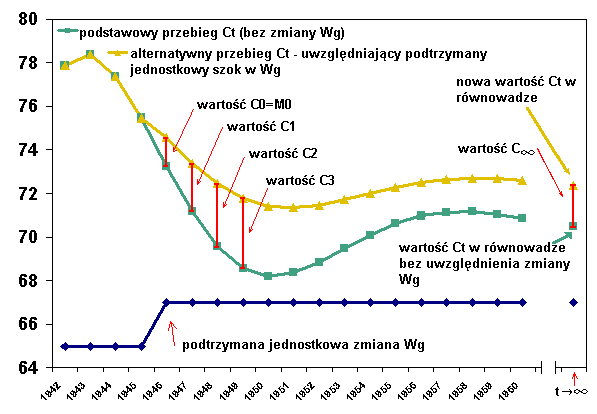
B. Wpływ podtrzymanego jednostkowego szoku w Wg (od 1946) na wartość C

Na powyższym rysunku zielona krzywa przedstawia podstawową trajektorię rozwoju zmiennej C przy ustalonych wartościach wszystkich zmiennych egzogenicznych. Żółta krzywa ilustruje A) wpływ zaburzenia impulsowego B) wpływ zaburzenia podtrzymanego w wartościach Wg (czyli przebieg żółtej krzywej wartości C odpowiada wartościom Wg według granatowej krzywej). Na rys. 2 wyraźnie jest uwidocznione znaczenie wartości mnożników.

Na rys. 2.B widzimy, że elementy mnożnika całkowitego C¥ możemy interpretować następująco: wzrost poziomu równowagi zmiennej Wg o jednostkę, przy niezmienionych poziomach równowagi innych zmiennych egzogenicznych, spowodowałby wzrost poziomu równowagi długookresowej zmiennej C o X jednostek. (ale pamiętajmy o przyjętym uproszczeniu roli zmiennej A, patrz także poniżej)

Próba interpretacji ekonomicznej:

sytuację na rysunku 2.A możemy interpretować jako coś w rodzaju „jednorazowej premii dla sfery budżetowej” – zastanawiamy się, jak taka premia zwiększy wielkość konsumpcji – zauważmy, że po kilku okresach przez pewien czas konsumpcja jest NIŻSZA niż w sytuacji braku podwyżki, po dłuższym czasie efekt wygasa – jak w przypadku zmian impulsowych w modelu stabilnym.

sytuacja na rys. 2.B odpowiada trwałej (np. ustawowej) zmianie podstawy wynagrodzenia w sferze budżetowej – widzimy, że efekt wzrostu konsumpcji jest permanentny. Analiza taka jak tu może być przydatna przy ustalaniu minimalnej wielkości „kiełbasy wyborczej” J

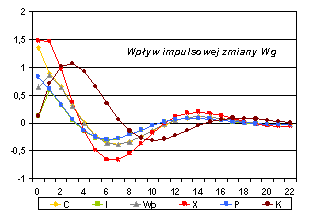
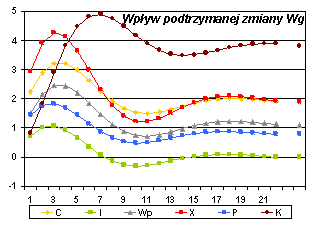
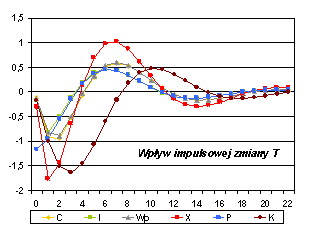
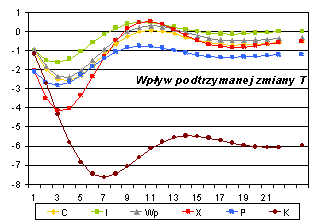
Poniżej przedstawione są odchylenia trajektorii zmiennych endogenicznych spowodowane przez impulsowe i trwałe zmiany wartości odpowiednich zmiennych egzogenicznych:

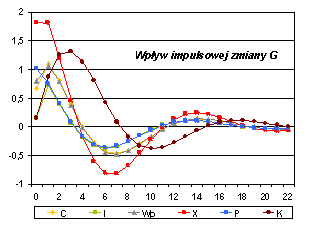
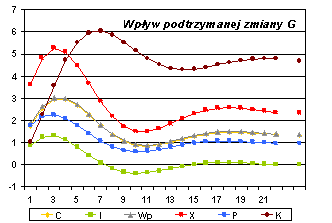
Rys. 3. ANALIZA MNOŻNIKOWA MODELU KLEINA – mnożniki pośrednie i skumulowane
Oceny mnożników M0 – M22 dla Wg	Oceny mnożników C1 – C22 i C¥ dla Wg
Oceny mnożników M0 – M22 dla G	Oceny mnożników C1 – C22 i C¥ dla G
Oceny mnożników M0 – M22 dla T	Oceny mnożników C1 – C22 i C¥ dla T
Oddzielne punkty na wykresach mnożników skumulowanych (prawa kolumna) to wartości mnożnika całkowitego C¥.

Zauważmy, że wpływ szoku (jednostkowego lub podtrzymanego), czyli odchylenia od trajektorii „bez szoku”, zilustrowany powyżej, ma charakter oscylacyjny (na przemian rosnący i malejący) , a nie jednostajny (monotoniczny). Miało to wyraźnie widoczny skutek na rys. 2.A – po początkowym wzroście konsumpcji nastąpił jej spadek (krótkotrwały i płytki, ale jednak). Taki „oscylacyjny” wpływ szoków ma związek z występowaniem zespolonych wartości własnych w macierzy D₁^. Jeśli wszystkie wartości własne są rzeczywiste (np. dla macierzy symetrycznych), to wpływ szoków ma charakter monotoniczny.

Stabilność modelu: c.d.

Spróbujmy jeszcze raz zastanowić się nad znaczeniem stabilności modelu. Stwierdziliśmy, że w modelu Kleina występują poziomy równowagi długookresowej zmiennych endogenicznych – przy ustalonych wartościach zmiennych egzogenicznych. Potraktowaliśmy jednak A (trend liniowy) jak zmienną egzogeniczną, której wartość ustalamy, co jest niezbyt konsekwentne. Jeżeli założymy (w sposób naturalny), że taki trend ma swoją kontynuację poza próbę, to oczywiście w modelu wystąpi długookresowy wzrost gospodarczy – zmienna W_p będzie miała komponent rosnący liniowo (więc nieograniczenie), co przeniesie się na pozostałe zmienne. Przy takim rozumieniu oczywiście nie ma miejsca na „poziomy równowagi” – mamy jakby „trend równowagi”. Jakie jest więc znaczenie stabilności modelu?

W modelu stabilnym wpływ jednorazowego szoku wygasa z upływem czasu (granicą ciągu mnożników pośrednich M_r jest macierz zerowa) a wpływ szoku podtrzymanego jest stabilny (po pewnym czasie ustala się - granicą ciągu mnożników skumulowanych C_r jest macierz C¥ zawierająca pewne stałe). W modelu niestabilnym wpływ jednorazowego szoku nie wygasa – zmienia znacząco całe „przyszłe” zachowanie systemu, macierz C¥ nie istnieje (nie jest macierzą skończonych stałych), nie można więc wyliczać oceny mnożnika całkowitego (innych tak). W praktyce zwykle ekonomiści spodziewają się stabilności modelu – własność mówiąca że nawet niewielkie zaburzenie z nieskończenie odległej przyszłości bardzo znacząco zmienia stan zmiennych w modelu wydaje się być odległe od standardowych intuicji. To nie znaczy że modele niestabilne są „do niczego”, ale raczej, że musimy sobie zdawać sprawę z czym mamy do czynienia i jak to wyjaśnić i rozumieć.

W modelu Kleina – jeśli uwzględnimy trend deterministyczny reprezentowany przez zmienną A także poza próbą – to przy ustalonych poziomach zmiennych egzogenicznych (innych niż A), startując z dowolnych wartości początkowych zmiennych endogenicznych, stan systemu dotrze i tak do „trendu równowagi”. Parametry tego „trendu równowagi” zależą od tego, jakie są poziomy równowagi zmiennych egzogenicznych. Gdyby model nie był stabilny, to startując z różnych początkowych wartości zmiennych endogenicznych system miałby zupełnie inne trajektorie nawet po długim czasie. Widzimy, że warunek początkowy możemy traktować tak samo jak ‘szok w okresie zerowym’ – czyli wpływ szoku i warunku początkowego jest taki sam.

Pewne rozszerzenie dla zainteresowanych:

Jeżeli chcemy badać zachowanie modelu dla bardziej skomplikowanych ścieżek zmiennych egzogenicznych (np. odpowiadających scenariuszom polityki gospodarczej) wykorzystujemy po prostu symulacje – możemy względnie łatwo wstawić do modelu dowolne wartości zmiennych egzogenicznych w kolejnych okresach. Symulację da się to zrobić nawet dla nieliniowego modelu (takimi się nie zajmowaliśmy, ale wszystko przed nami). Można nawet losować sobie pseudo-realizacje składników losowych (z rozkładu odpowiadającego oszacowanej macierzy kowariancji składników losowych), powtarzać to przy wielu przebiegach i zrobić histogram wartości interesującej nas zmiennej endogenicznej w rozważanym okresie - w ten sposób uwzględniamy niepewność wynikającą ze struktury stochastycznej modelu. Jeżeli dodatkowo będziemy losować parametry (np. z rozkładu normalnego o wartości oczekiwanej równej ocenom parametrów i macierzy kowariancji równej ocenie asymptotycznej macierzy kowariancji estymatora np. 2MNK) to uwzględnimy także niepewność wynikającą z błędu estymacji. Ale to raczej materiał na cały przedmiot, mają Państwo w programie „prognozowanie i symulacje” – to powinno się tam znaleźć JJJ

Najczęściej spotykane w zadaniach błędy:

-źle odwrócona macierz B (często zapomina się o transpozycji) – proszę ZAWSZE sprawdzić, czy BB^-1=I

-źle zrobiona macierz D₁^ – proszę się upewnić, że elementy wstawiają Państwo we właściwe wiersze D₁^ (kolejność wierszy wynika z kolejności kolumn)

-zła interpretacja ocen mnożników (mieszanie procentów z jednostkami)

-zapominanie o daszkach – w praktyce mamy do czynienia z ocenami mnożników, D₁ etc. – ja tutaj w niektórych miejscach pisałem, zakładając, że znamy PRAWDZIWE wartości parametrów, więc nie było daszków.

UWAGI BIBLIOGRAFICZNE

Gdyby Państwo chcieli poczytać coś strawnego i lekko napisanego o zastosowaniu modeli wielorównaniowych we współczesnej makroekonometrii (do prognozowania, bo to główny cel) – to bardzo interesujący temat – polecam artykuł:

Diebold F.X. (1998) The Past, Present, and Future of Macroeconomic Forecasting, Journal of Economic Perspectives, vol 12, n. 2 (spring 1998) ss. 175-192.

Mają tam Państwo opisane wzloty i upadki zastosowań modeli wielorównaniowych (i ich alternatywy); artykuł jest przy tym napisany względnie prostym językiem. J

Zadanie Laboratoryjne

Wykorzystując wyniki estymacji 2MNK modelu Kleina proszę dokonać analizy mnożnikowej. Proszę wyliczyć oceny mnożników M oraz C do rzędu 15 włącznie (w dodatku matrix 1.5 jest funkcja potęgowania macierzy co może trochę pomóc) oraz zbadać stabilność modelu a także wyliczyć ocenę mnożnika całkowitego. Proszę sporządzić po jednym wykresie obrazującym wpływ podtrzymanej/impulsowej zmiany wybranej zmiennej egzogenicznej (przy pozostałych niezmienionych).