Zajęcia 17

Uogólniony Model (Normalnej) Regresji Liniowej - UM(N)RL

W niniejszych zajęciach rozpatrujemy zagadnienie uchylenia 5 założenia KMRL:

w KMRL mieliśmy V(e) = s² I, w UMRL przyjmujemy: V(e) = s² W

(pozostałe założenia bez zmian!!)

streszczenie odcinka:

(wracamy do modeli jednorównaniowych, ale komplikujemy strukturę stochastyczną)

1) 5 zał. KMRL definiuje pewne „przyjazne” własności składników losowych. W praktyce spodziewamy się jednak, że składniki losowe mogą mieć pewne „kłopotliwe” własności, co sprawia, że musimy uchylić założenie V(e) = s² I

2) po uchyleniu 5 założenia KMRL estymator MNK będzie miał inne własności niż w KMRL (gorsze): straci efektywność, poza tym standardowe procedury wnioskowania KMRL/KMNRL tracą zastosowanie (wzory mają inną postać)

3) będziemy szukać więc innego estymatora o „lepszych” własnościach (efektywnego) oraz sposobu na prowadzenie wnioskowania (wyliczanie błędów średnich szacunku, testowanie hipotez)

a) przyjmując pewne nierealistyczne założenie znajdziemy taki efektywny i pozwalający na wnioskowanie estymator – Uogólnionej MNK (UMNK)

b) potem postaramy się uchylić nierealistyczne założenie: otrzymamy w ten sposób nowy estymator (Estymowanej UMNK: EUMNK), będziemy chcieli żeby zachował on dobre własności estymatora UMNK (efektywność): to się uda asymptotycznie (dla T®¥) i przy pewnych dodatkowych założeniach

[będziemy więc mieli trzy różne estymatory: MNK, UMNK, EUMNK – każdy o innych własnościach]

4) aby wykorzystać w praktyce estymator EUMNK, musimy określić, jakiego rodzaju „kłopot” mamy ze składnikami losowymi. Do estymatora EUMNK wstawiamy wtedy odpowiednie funkcje. Ponadto będziemy potrzebować testu, pozwalającego stwierdzić, czy rzeczywiście taki akurat problem ma miejsce.

(w tych zajęciach mamy sporo wzorów które się minimalnie różnią, proszę uważać na notację!!)

1. Rozszerzenie założeń KMRL: dlaczego chcemy uchylić 5 założenie?

W Klasycznym Modelu Regresji Liniowej przyjmuje się (5°), że macierz kowariancji składnika losowego e_t ma postać: s²I. To implikuje dwie własności składników losowych:

a) składniki losowe różnych obserwacji są nieskorelowane [cov(e_t, e_s) = 0 dla t ¹ s] – to brak autokorelacji składników losowych.

b) wariancja składnika losowego jest taka sama dla każdej obserwacji [var(e_t)= s² (t = 1,2,...,T)] – ta własność to homoskedastyczność składników losowych

W praktyce często możemy się spodziewać, że założenia te mogą nie być spełnione. W szczególności:

a) w przypadku danych w postaci szeregów czasowych spodziewamy się wystąpienia autokorelacji składników losowych – przypuszczamy, że wystąpienie bardzo silnego zaburzenia (jak klęska żywiołowa, wojna etc.) – czyli „wylosowanie” bardzo dużego e_t – będzie oddziaływać również na następne („sąsiednie”) obserwacje – czyli, że może występować skorelowanie składników losowych różnych obserwacji

b) w przypadku danych przekrojowych – tj. obserwacji pochodzących z różnych obiektów z tego samego okresu – może wystąpić heteroskedastyczność – wariancja składnika losowego może nie być taka sama w całej próbie. Jeżeli obserwujemy produkcję w grupie hut obejmujących zarówno niewielkie zakłady jak i olbrzymy, możemy oczekiwać, że wariancja losowych zakłóceń w grupie zakładów dużych będzie większa niż w grupie zakładów małych (jeśli składnik losowy jest addytywny)

c) w danych panelowych (z różnych obiektów w różnych okresach czasu) spodziewamy się zarówno autokorelacji jak i heteroskedastyczności skł. losowych.

Jak widać struktura macierzy kowariancji składnika losowego typu s²I może okazać się zbyt mocna. Rozważa się w związku z tym jej uogólnienie. W tym celu rozpatrujemy model, w którym V(e) = s² W, gdzie W jest pewną macierzą kwadratową, symetryczną i dodatnio określoną. Zauważmy, że skalar s² jest tu parametrem skali (skaluje wariancje i kowariancje elementów e), natomiast macierz W wyznacza strukturę V(e) – korelacje między różnymi składnikami losowymi e zależą wyłącznie od elementów W (s² z wariancji i kowariancji się uprości).

Wstawienie V(e) = s² W zamiast V(e) = s² I odpowiada przejściu od KMRL do UMRL czyli Uogólnionego Modelu Regresji Liniowej

Ponieważ rozważamy macierze kowariancji, to warto przypomnieć, że ogólnie dla wektora losowego y: V(y)=E{[y-E(y)][y-E(y)]′}; jeżeli rozpatrujemy tu macierz kowariancji wektora składników losowych, którego wartość oczekiwana jest wektorem zerowym, to V(e) = E(ee′) – zakładamy tu, że wszystkie wektory są kolumnowe.

Postać macierzy W określa strukturę stochastyczną modelu – własności składników losowych.

2. Jakie są konsekwencje założeń UMRL dla estymatora MNK i stosowanych w KM(N)RL procedur wnioskowania?

W KMRL obowiązuje tw. Gaussa i Markowa o estymatorze MNK – jest on liniowy, nieobciążony i efektywny w klasie liniowych oraz nieobciążonych. Ponieważ uchylamy 5 założenie, twierdzenie nie zachodzi. Pamiętamy jednak, że dowód NIEOBCIĄŻONOŚCI wymaga tylko założeń 1-4, które mają w UMRL tę samą postać. Dowód EFEKTYWNOŚCI w klasie... (czyli najmniejszej wariancji spośród estymatorów danej klasy) wymaga wszystkich 5 założeń. W UMRL estymator MNK traci efektywność, pozostaje liniowy i nieobciążony. Wobec tego możemy go stosować dla uzyskania ocen punktowych parametrów, choć co prawda wolelibyśmy mieć estymator efektywny.

Niestety sytuacja jest gorsza, kiedy chcemy sobie policzyć coś więcej niż tylko oceny punktowe. Błędy średnie szacunku wyliczamy jako pierwiastki kwadratowe z elementów przekątniowych oszacowanej macierzy kowariancji estymatora MNK:

w KMRL:

wykorzystujemy nieobciążony estymator macierzy kowariancji estymatora MNK: dany wzorem .

Przypomnijmy, że dla uzyskania tego wzoru łączymy dwa fakty:

1) na mocy twierdzenia Gaussa i Markowa macierz kowariancji estymatora MNK ma postać:

2) na mocy twierdzenia o wariancji resztowej, nieobciążonym estymatorem s² jest s².

niestety, kiedy uchylimy 5 założenie KMRL ani 1) ani 20 nie zachodzą:

w UMRL:

- (macierz kowariancji estymatora MNK ma inną postać)

- (wariancja resztowa nie jest nieobciążonym estymatorem s²)

widzimy więc, że co prawda mamy pod ręką nieobciążony estymator nieznanych parametrów, ale niestety nie możemy (stosując wzory z KMRL) policzyć nawet błędów średnich szacunków (nie mówiąc już o testowaniu, przy założeniu normalności składników losowych).

W związku z tym szukamy:

-efektywnego nieobciążonego estymatora b.

-estymatora macierzy kowariancji tego estymatora (lub estymatora MNK) pozwalającego wyliczyć błędy średnie szacunku oraz prowadzić testy

3. Jak znaleźć w UMRL efektywny estymator b i estymator jego macierzy kowariancji?

Aby znaleźć w UMRL efektywny estymator, a także znaleźć i oszacować jego macierz kowariancji, analizę rozbija się na dwa etapy:

1. Zakładamy, że macierz W jest znana, i przy tym założeniu wyprowadzamy estymator i badamy jego własności. Takiego estymatora nie da się praktycznie zastosować (bo praktyce W jest nieznana), ale da się elegancko wyprowadzić jego własności.

2. Rozważamy więc sposób szacowania W oraz zastanawiamy się, do jakiego stopnia estymator zbudowany analogicznie jak w punkcie 1, tylko z oszacowaną macierzą W utrzyma własności.

Będziemy więc mieli dwa nowe estymatory:

1: ze znaną W (to konstrukcja czysto teoretyczna, ale naprowadzająca nas na rozwiązanie problemu),

2: z szacowaną W (ten estymator można stosować, jednak wymaga to dodatkowo podania estymatora W)

3. A. Analiza przy znanej macierzy W

Aby wyprowadzić postać szukanego estymatora w UMRL, rozpatrzymy pewne przekształcenie modelu UMRL w taki sposób, że spełnione będą założenia KMRL, natomiast nieznane parametry będą te same. W przekształconym modelu zachodzi twierdzenie Gaussa i Markowa, więc zapisujemy tam estymator MNK nieznanych parametrów. Potem uwzględniamy wykorzystane przekształcenie zmiennych „w drugą stronę” otrzymujemy estymator nieznanych parametrów w wyjściowym modelu (UMRL), mający ponadto własności MNK w KMRL: najlepszy wśród liniowych i nieobciążonych. Tak samo możemy znaleźć w przekształconym modelu postać macierzy kowariancji uzyskanego estymatora, i jej estymator, co po wykorzystaniu przekształcenia ‘z powrotem’ pozwoli na prowadzenie wnioskowania jak w KMRL/KMNRL.

Dokładniej:

1) nieosobliwą macierz W można zawsze przedstawić poprzez W^-1= P′P (macierz P grupuje pewne znane stałe)

2) w miejsce modelu

(a) y = Xb+e ,

rozpatrujemy model:

(b) Py = PXb+Pe

więc w modelu (b):

-co prawda przekształcono zmienne objaśniające (PX zamiast X), objaśniane (Py zamiast y) i składniki losowe (Pe zamiast e), ale wektor nieznanych parametrów b jest TEN SAM co w modelu wyjściowym – więc uzyskany w (b) estymator będzie estymatorem nieznanych parametrów (a)

oraz

-spełnione są założenia KMRL , bo:

>składnik losowy w modelu (b) to Pe , jego macierz kowariancji to E[Pe(Pe)′] = E[Pee′P′] = PE[ee′]P′

a ponieważ E[ee′] =s² W , to PE[ee′]P′= s² PWP′= s² PWP′I= s² PWP′(PP^-1) =s² PWW^-1P^-1 = s²I.

>jeżeli e ma rozkład normalny, to także Pe (jako liniowa nieosobliwa transformacja) ma rozkład normalny (zał. 6 jeśli jest)

>do e nic nie dodajemy, więc jego wartość oczekiwana to E[Pe] = P E[e] = P * 0 = 0 (spełnione zał. 4)

>macierz P jest nieosobliwa, więc PX ma pełen rząd kolumnowy (spełnione zał. 3)

>macierz P jest znana, bo W jest znana, więc PX jest nielosowa. (spełnione zał. 2)

> Py = PXb+Pe (spełnione zał. 1)

Zapisując estymator MNK w modelu (b) uzyskujemy:

= [(PX)′PX]^-1(PX)′Py = (X′P′PX)^-1X′P′Py = (X′W^-1X)^-1X′W^-1y.

jest to estymator Uogólnionej MNK – czyli GLS (od Generalized Least Squares) – to estymator wektora b przy znanej macierzy W - w nad W nie ma daszka.

Podobnie możemy wyprowadzić postać jego macierzy kowariancji:

V() = s² (X′P′PX)^-1= s² (X′W^-1X)^-1

Własności : ponieważ w (b) spełnione są założenia KMRL i zachodzi twierdzenie Gaussa i Markowa; więc:

W UMRL estymator UMNK (tj. przy znanej macierzy W) dany wzorem o macierzy kowariancji: jest najlepszy w klasie estymatorów liniowych i nieobciążonych. (to tzw. twierdzenie Aitkena, które jest wnioskiem z tw. Gaussa i Markowa)

udało się nam więc uzyskać efektywny estymator b. Aby wyliczyć coś więcej niż tylko oceny parametrów, musimy mieć estymator macierzy kowariancji . Potrzebujemy więc estymatora s². W modelu (b) , jeśli dodatkowo założymy T > k, zachodzą założenia twierdzenia o wariancji resztowej.

W KMRL suma kwadratów reszt MNK ma postać: (y-Xb^)′(y-Xb^). W UMRL jej odpowiednikiem jest:

(Py-PX)′(Py-PX) = [P(y-X)]′P(y-X) = (y-X)′P′P(y-X) = (y-X)′W^-1(y-X)

Zauważmy, że jest to suma kwadratów reszt „ważona” macierzą W^-1 – w zwykłej MNK ta macierz ważąca jest implicite równa macierzy jednostkowej. Wobec tego (wniosek z twierdzenia o wariancji resztowej):

W UMRL nieobciążonym estymatorem s² jest uogólniona wariancja resztowa wykorzystująca sumę kwadratów reszt daną powyżej:

,

Nieobciążonym estymatorem macierzy kowariancji estymatora UMNK w UMRL jest:

(przy znanej macierzy W)

estymator jest nieobciążony, bo mamy nieobciążony estymator jedynego nieznanego elementu czyli , więc:

Do szczęścia brakuje nam jeszcze postaci macierzy kowariancji estymatora zwykłej MNK w UMRL (jak pamiętamy z punktu 2 powyżej, znany z KMRL wzór nie jest prawdziwy w UMRL). Aby ją otrzymać policzmy:

V()=E{[-E()][- E()]′}=E[(- b)(- b)′]=

(w ostatniej równości wykorzystujemy nieobciążoność także w UMRL)

= E{[(X′X)^-1X′y-b][(X′X)^-1X′y-b]′}= E{[(X′X)^-1X′(Xb+e)-b][(X′X)^-1X′(Xb+e)-b]′} =

= E{[b+(X′X)^-1X′e)-b][(b+ (X′X)^-1X′e - b]′} = E{[(X′X)^-1X′e][e′X(X′X)^-1]} = (X′X)^-1X′ E(ee′)X(X′X)^-1=

=s²(X′X)^-1X′WX(X′X)^-1

Estymator tej macierzy budujemy analogicznie jak , tak samo dowodzimy jego nieobciążoności. Ostatecznie:

W UMRL macierz kowariancji estymatora zwykłej MNK ma postać: ,

a jej nieobciążonym estymatorem jest

(przy znanej macierzy W)

Zauważmy, że ponieważ KMRL jest szczególnym przypadkiem UMRL, w którym: W = I, wszystkie dane wyżej wzory „zwijają się” do znanej z KMRL postaci po podstawieniu W = I. Pozwala to choć w przybliżeniu sprawdzić czy dobrze się je pamięta.

Podsumowując:

Przy znanej macierzy W mamy do dyspozycji estymatory

- zwykłej MNK (OLS) – liniowy i nieobciążony

- Uogólnionej MNK (GLS) – najlepszy w klasie liniowych i nieobciążonych

W UMRL przy znanej macierzy W estymator UMNK jest jednoznacznie preferowany w stosunku do estymatora zwykłej MNK - ponieważ ten pierwszy ma mniejszą wariancję. Niestety w praktyce żadnego z przedstawionych w punkcie 3.A. estymatorów nie możemy użyć, bo nie znamy postaci W. Mamy więc do czynienia z problemem którym jest:

3. B. Analiza przy nieznanej macierzy W - własności ogólne

W praktyce niestety macierz W nie jest znana – jej znajomość to bardzo silne założenie – odpowiada znajomości wszystkich korelacji oraz ilorazów wariancji dla wszystkich elementów wektora składników losowych e. Trudno założyć, że je znamy. Co w takim razie zrobić? Narzuca się prosta odpowiedź: szacować macierz W i jej ocenę wstawić do wzorów danych powyżej. Pojawiają się w związku z tym dwa dalsze pytania:

- jak oszacować W?

- czy nowy estymator, uzyskany z UMNK poprzez zastąpienie W jej oszacowaniem , zachowa pożądane własności estymatora UMNK (zwłaszcza efektywność)?

Można zauważyć, że nie wchodzi w grę w pełni swobodne szacowanie W - ma ona wymiar T na T i zawiera (na mocy symetrii) (T²-T)/2 + T nieznanych parametrów – czyli o (T²-T)/2 więcej niż mamy obserwacji. W związku z tym szacowanie macierzy W musi wykorzystywać jakąś dodatkową zadaną a priori informację.

Zagadnienie szacowania macierzy W można przedstawić następująco: jeśli nie można szacować wszystkich nieznanych elementów W, bo w ogólnym przypadku zawiera ona za dużo swobodnych parametrów, załóżmy pewną strukturę W, będącej funkcją względnie niewielu nieznanych parametrów, które potem oszacujemy i te oszacowania wykorzystamy. Potrzebujemy więc:

a) W jako funkcji macierzowej wektora parametrów – czyli W = W(j) [pewnej struktury W]

b) estymatora wektora parametrów j czyli .

Mając te dwa elementy możemy uzyskać ocenę macierzy W jako:

Wstawiając ocenę W do wzoru na estymator UMNK uzyskamy nowy estymator, „UMNK z szacowaną macierzą W”, zwany FGLS lub EGLS (od feasible GLS – wykonalny UMNK lub estimable GLS – EGLS) a po polsku EUMNK: estymowana UMNK. Zapiszemy go jako:

, ewentualnie

Nasuwa się teraz pytanie: jakie są własności estymatora EUMNK , a zwłaszcza, czy zostanie zachowana własność efektywności?

W UMRL:

Estymator EUMNK jest nieobciążony (ale przy pewnych specjalnych warunkach danych niżej dla zainteresowanych)

Estymator EUMNK nie jest już estymatorem liniowym (np. dlatego, że sensowny jest funkcją y)

Przy pewnych założeniach (dosyć skomplikowanych do wyłożenia) można pokazać, że EUMNK ma pożądane własności asymptotyczne – czyli dla (T ® ¥), w szczególności:

- jest zgodny

- jest asymptotycznie bardziej efektywny od estymatora zwykłej MNK

Warunki które zapewniają zachowanie tych własności można przedstawić (nie w pełni dokładnie) następująco

-W(j) jest „dobrze dobrana” – dobrze odwzorowywała prawdziwą W,

- jest zgodnym estymatorem j,

pozwala to uzyskać zgodny estymator W jako

Warunek wystarczający nieobciążoności estymatora EUMNK: (dla ciekawych)

jeżeli składniki losowe mają rozkład symetryczny wokół zera, oraz - czyli estymator j jest parzystą funkcją wektora reszt (i przy dodatkowym założeniu, że wartość oczekiwana istnieje), to estymator EUMNK jest nieobciążony.

Interesujące jest, że zgodność wystarczy do asymptotycznej efektywności EUMNK (nie jest potrzebna asymptotyczna efektywność ) {oczywiście to nieformalny zarys, ścisłe potraktowanie sprawy można znaleźć w podręcznikach}

Zauważmy, że EUMNK jest procedurą estymacji dwustopniowej: w pierwszym kroku szacujemy macierz W (wykorzystując zwykle do tego oceny zwykłej MNK parametrów), w drugim kroku wyliczamy dopiero oceny parametrów EUMNK.

Przy nieznanej i szacowanej macierzy W porównanie pomiędzy estymatorem zwykłej MNK a estymatorem EUMNK nie jest takie oczywiste. Po pierwsze odwołujemy się do własności asymptotycznych; własności EUMNK w małej próbie nie są w ogólnym przypadku znane (mamy co prawda warunek wystarczający nieobciążoności, ale interesuje nas w szczególności efektywność), w konkretnych przypadkach mogą być badane symulacyjnie. Przy podanych wyżej warunkach, rozkład asymptotyczny estymatora EUMNK jest taki jak rozkład estymatora UMNK. W szczególności:

W UMRL i przy pewnych warunkach dodatkowych (jak te podane wyżej):

Asymptotyczna macierz kowariancji estymatora EUMNK ma postać:

a jej zgodnym estymatorem jest:

przy czym:

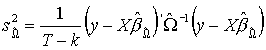
Przypomnijmy, że podstawową przewagą UMNK nad MNK w UMRL jest efektywność UMNK. W przypadku EUMNK mamy dwa dodatkowe źródła „zakłóceń”:

– estymator może w małej próbie „źle trafić” – jego realizacja jest odległa od „prawdziwego” j przez co wnosi nieprawdziwą informację i pogarsza własności ocen zamiast je polepszać.

– Prawdziwa struktura W(j) jest inna niż przyjęta przez nas – czyli występuje błąd specyfikacji. Trudno jest poznać „prawdziwą” strukturę macierzy kowariancji składników losowych – możemy mieć pewne przekonania co do niektórych jej własności (np. możemy czasem rozsądnie oczekiwać autokorelacji), ale tu konieczne jest podanie dokładnej struktury W(j) (dokładnej postaci autokorelacji) – łatwo więc o błąd.

Podsumowując, w małej próbie i przy szacowanej macierzy W (czyli w praktyce) zakłócenia mogą zniwelować korzyści i przewaga EUMNK nad MNK nie jest tak jednoznaczna i jasna – w pewnych szczególnych przypadkach mimo tego, że dopuszczamy W ¹ I, zwykła MNK może być przynajmniej tak dobra jak EUMNK.

W UMRL możemy w związku z tym chcieć wyliczyć ocenę macierzy kowariancji zwykłej MNK:

W UMRL i przy pewnych warunkach dodatkowych (jak te podane wyżej):

zgodnym estymatorem macierzy kowariancji estymatora zwykłej MNK jest:

UWAGI DODATKOWE:

A. wnioskowanie w UMNRL

Jeżeli spełnione jest założenie 6 o normalności składników losowych (jak w KMNRL), to estymator EUMNK ma asymptotyczny rozkład normalny, i możemy procedury wnioskowania analogiczne jak w KMNRL stosować w przybliżeniu (sytuacja jest podobna jak w przypadku regresji z losowymi zmiennymi objaśniającymi przypadek 2 lub w MNRN). Oczywiście wykorzystujemy .

W związku z tym przy wyliczaniu np. błędu średniego szacunku dla liniowej kombinacji parametrów zamiast wzoru powinniśmy użyć: .

B. Losowe zmienne objaśniające

Jeżeli nie jest spełnione założenie 2 to sprawy mogą się skomplikować. Macierz X losowa ale niezależna stochastycznie od wszystkich epsilonów powoduje analogiczną zmianę własności jak w przypadku regresji z losowymi zmiennymi objaśniającymi przypadek A, co praktycznie nie ma dla nas większego znaczenia.

Jednak prawdziwe kłopoty zaczynają się, gdy mamy do czynienia z opóźnieniami y po prawej stronie równania regresji. Jeśli jednocześnie wystąpi autokorelacja składników losowych (macierz W nie będzie diagonalna), będziemy mieć do czynienia z regresją z losowymi zmiennymi objaśniającymi przypadek C (przypadkiem analogicznym do procesu autoregresyjnego z zależnymi składnikami losowymi – por. wykład). Wtedy estymator zwykłej MNK jest NIEZGODNY, natomiast estymator EUMNK jest zgodny. Musimy oczywiście odpowiednio dopasować procedurę uzyskiwania zgodnej oceny j.

4. Analiza przy znanej macierzy W - przypadki szczególne

Zastosowanie EUMNK wymaga zadania struktury macierzy W czyli funkcji W(j) oraz znalezienia zgodnego estymatora: .

Na samym początku odwołaliśmy się do dwóch cech W odpowiadających spodziewanym w pewnych przypadkach własnościom składników losowych: heteroskedastyczności i autokorelacji. Uzasadniona wydaje się więc następująca strategia postępowania:

1. Rozważenie, które z tych zjawisk (i w jakiej formie) może wystąpić w naszym problemie

2. Zastosowanie testu pozwalającego na formalne zbadanie występowania tej własności

3. Jeśli test ją odrzuci (nie przyjmie), to możemy zastosować zwykłą MNK i na tym poprzestać (jeśli estymator MNK jest zgodny – w pewnych szczególnych przypadkach może nie być)

4. Jeśli test nie odrzuci (lub przyjmie) występowanie rozważanej własności, to

A) staramy się zbudować taką strukturę W(j) która ją odzwierciedla

B) szukamy zgodnego estymatora j

C) jeśli mamy A i B, stosujemy EUMNK (FGLS)

Oczywiście możemy w punkcie C zastosować zwykłą MNK zgodnie z dyskusją powyżej sugerującą, że w przypadku szacowania W przewaga EUMNK nad MNK nie jest oczywista i bezwzględna. Jednakże, gdy W bardzo odbiega od macierzy jednostkowej i jesteśmy przekonani, że dobrze modelujemy strukturę macierzy kowariancji e, zysk na stosowaniu EUMNK może być znaczny. Dlatego dla decyzji czy stosować EUMNK czy MNK istotny może być wynik testu. Silne odrzucenie W = I przemawia za stosowaniem EUMNK.

Chcemy szacować macierz kowariancji składników losowych (z dokładnością do skalara s²) i testować jej własności – czyli wnioskować o e które są nieobserwowalne. Naturalne wydaje się wykorzystanie w tym celu reszt zwykłej MNK czyli e^. Często zarówno test jak i estymator j wykorzystują właśnie reszty MNK. UWAGA! Ten sposób postępowania można stosować tylko wtedy, gdy estymator MNK jest zgodny. Kiedy na przykład może nie być zgodny? Gdy występuje autokorelacja ORAZ w regresji objaśniające (po prawej stronie) są opóźnione wartości y (jak w regresji z losowymi zmiennymi objaśniającymi przypadek z przykładem procesów autoregresyjnych) – w takim przypadku opisana procedura musi być zmodyfikowana.

Poniżej przedstawimy typowe elementy zarysowanego schematu w prostym przypadku autokorelacji składników losowych. Przypadek heteroskedastyczności oraz występowania zarówno autokorelacji jak i heteroskedastyczności nie będą tak szczegółowo rozważane. Zainteresowanych testowaniem tych własności i estymacją przy ich występowaniu mogę odesłać do literatury.

EUMNK w przypadku autokorelacji składników losowych typu AR(1)

MODEL:

y_t = x_tb+e_t

e_t = j e_t-1 + x_t ; -1 < j < 1

x_t~iiN(0, s²_x)

(czyli proces autoregresyjny rzędu 1 [Ar(1)] dla składników losowych – mają one zerową wartość oczekiwaną – więc proces AR(1) jest bez wyrazu wolnego; normalność nie jest potrzebna od razu tylko później.)

w takim modelu:

STRUKTURA W(j) odpowiadająca AR(1) dla e:

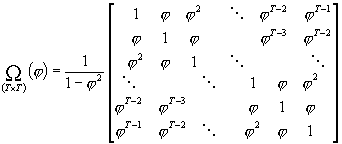
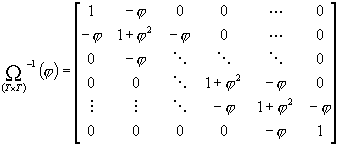
s²_x przejmuje rolę s² w zał. UMRL

TEST Durbina – Watsona

Na podstawie reszt zwykłej MNK z regresji która MUSI zawierać wyraz wolny.

Statystyka testowa:

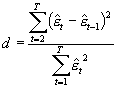
H₀: brak autokorelacji dodatniej składników losowych typu AR(1) (j = 0)

H₁: występuje autokorelacja dodatnia składników losowych typu AR(1) ( 0 <j < 1)

d przyjmuje wartości od 0 do 4.

Przyjmujemy = 1- d/2 [tak można otrzymać zgodny estymator j]; wobec tego łatwo skojarzyć wartości j z odpowiadającymi im wartościami d i interpretacją wyniku testu:

d bliskie 0 (j bliskie 1) świadczy za autokorelacją dodatnią

d równe 2 (j bliskie 0) świadczy o braku autokorelacji (KMNRL)

d bliskie 4 (j bliskie -1) świadczy za autokorelacją ujemną

Rozkład statystyki d przy prawdziwości H₀ jest niestandardowy – zależy od dokładnej postaci macierzy X - i nie znamy dokładnych wartości krytycznych – znamy tylko ich przedział. Wartości krytyczne są pomiędzy D_L a D_U danymi w tablicach.

(Np. tu: http://www.ses.man.ac.uk/clark/es561/tables.pdf ) tylko D_U i D_L są osobno.

(wynika to z faktu, że rozkład statystyki DW zależy od konkretnej postaci X. Można na szczęście podać przedział, w którym znajduje się wartość krytyczna „niezależnie od tego, jaki jest X”. Wiemy więc, że prawdziwa wartość krytyczna jest gdzieś pomiędzy D_U i D_L

Ponieważ d bliskie zeru świadczy przeciwko H₀, to:

d w zakresie (0, D_L) => odrzucamy H₀ o braku autokorelacji dodatniej

d w zakresie (D_L, D_U) => test jest niekonkluzywny

d większe od D_U => nie ma podstaw do odrzucenia H₀

Jeżeli nie odrzucimy H₀ (braku autokorelacji dodatniej), wyliczamy d′ = 4 – d i testujemy tak samo, zamieniając słowo „dodatnia” na „ujemna”. Kiedy nie odrzucimy braku autokorelacji przeciwko alternatywom zarówno dodatniej, jak i ujemnej, możemy roboczo przyjąć, że autokorelacja nie występuje.

Kiedy odrzucamy hipotezę o braku autokorelacji na rzecz autokorelacji dodatniej lub ujemnej – czyli przyjmujemy występowanie autokorelacji – powinniśmy stosować estymator EUMNK zamiast MNK.

Kiedy nie ma podstaw do odrzucenia braku autokorelacji dodatniej i ujemnej, możemy stosować zwykłą MNK – korzyść z UMNK będzie niewielka i może być całkowicie zniwelowana przez np. zachowanie estymatora j w małej próbie.

Kiedy test jest niekonkluzywny – roboczo możemy przyjąć, że argumenty na rzecz MNK i EUMNK się równoważą i możemy stosować dowolną z tych metod.

ZGODNA ESTYMACJA j:

A) Wykorzystując statystykę d: = 1- d/2

B) Można też zrobić regresję reszt MNK na ich opóźnieniach zgodnie z e_t = j e_t-1 + x_t i , wykorzystać reszty MNK w miejscu e_t i szacować j stosując zwykłą MNK.

Wszystko jedno, który ZGODNY estymator j wybierzemy, bo potrzebujemy zgodności właśnie a pod tym względem są one takie same. Wyniki w małej próbie dla różnych zgodnych estymatorów j będą się numerycznie różnić.

Dalej już normalna estymacja EUMNK wykorzystująca wszystkie powyższe informacje. Analityczna postać macierzy W i W^-1 jest dana, by nie odwracać ich numerycznie, co generuje dodatkowe błędy.

EUMNK w przypadku heteroskedastyczności składników losowych

Dla rozważania prostego przypadku heteroskedastyczności zakładamy, że próbę można podzielić na dwie grupy – w pierwszej grupie T₁ obserwacji wariancja e wynosi s²₁, w drugiej, liczącej T₂ obserwacji, wynosi ona s²₂. Odpowiada to następującej strukturze V(e):

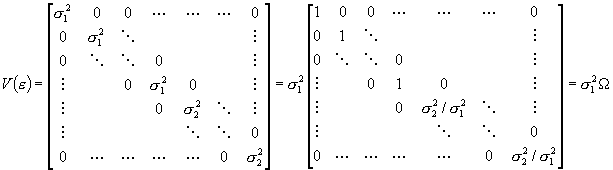
Tutaj W to ostatnia macierz przed ostatnim znakiem równości.

(oczywiście na przekątnej elementów s²₁ jest T₁ i zakładamy, że obserwacje z pierwszej grupy stanowią górny blok (o T₁ wierszach) w wektorze y i macierzy X)

Przy założeniach UMNRL, możemy wyprowadzić test pozwalający nam porównać wariancję e w obydwu grupach obserwacji. Ponieważ w ramach podgrupy wariancja jest stała, szacujemy zwykłą MNK obydwie podgrupy obserwacji OSOBNO, uzyskując oceny parametrów oraz s²₁ i s²₂. Chcemy testować, czy stosunek s²₁/s²₂ jest istotnie różny od 1.

Ponieważ będziemy stosować test jednostronny, musimy zdecydować, która z wariancji powinna być większa. Oznaczmy ją s²_W – pozostała to s²_M (czyli za M i W podstawiamy 1 lub 2 w zależności od tego, w której grupie występuje większa wariancja składników losowych)

Stawiamy hipotezy:

H₀: s²_W = s²_M Û s²_W/s²_M = 1 (brak heteroskedastyczności)

H₁: s²_W > s²_M Û s²_W/s²_M > 1 (występuje heteroskedastyczność, wariancja składników losowych w grupie W jest większa)

Przy prawdziwości H₀, statystyka

F_emp = s²_W/s²_M

ma rozkład F(T_W - k,T_M - k).

Jeżeli uzyskamy realizację Femp > Fkryt na ustalonym poziomie istotności, powinniśmy stosować EUMNK. Postać macierzy W wynika z postaci V(e) danej powyżej. Aby uzyskać W^, zastępujemy iloraz s²₂/s²₁ przez s²₂/s²₁. Jeżeli w drugiej grupie obserwacji wariancja e jest większa, to ten iloraz to F_emp. Jeśli zachodzi sytuacja przeciwna, to iloraz s²₂/s²₁ to odwrotność F_emp. Analityczna postać W^^-1 jest podobna do postaci W^; jedynie w drugiej części głównej przekątnej zamieniamy ilorazy na ich odwrotności – wynika to z diagonalnej postaci macierzy W:

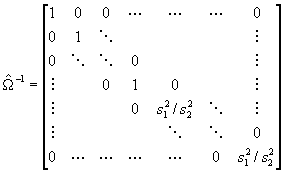
s²₁/s²₂ pełni tu rolę parametru j. W ten sposób możemy zastosować EUMNK.

Problemem w zastosowaniu tej metody jest konieczność arbitralnego podziału obserwacji na dwie grupy – rozważając różne podziały uzyskamy różne wyniki; zakładamy też, że w ramach podgrupy wariancja składników losowych jest stała.

Powyższe szczególne przypadki postaci macierzy W i związane z nimi testy oraz estymatory W^ to tylko pewne proste przykłady mające zilustrować problem. W praktyce rozważa się bardziej złożone modele dla składników losowych i bardziej zaawansowane metody szacowania V(e).

Ćwiczenie Excelowe czyli zadanie domowe

Na danych maddala.xls proszę oszacować funkcję C-D (statyczną) zwykłą MNK. Następnie proszę rozważając autokorelację AR(1) lub heteroskedastyczność składników losowych:

1. przeprowadzić test Durbina i Watsona / test na stałość wariancji skł. losowych (na użytek HETEROSKEDASTYCZNOŚCI przyjmując jedną grupę obserwacji do 1946 włącznie, drugą od 1947) i w każdym przypadku:
2. oszacować j zgodnym estymatorem
3. wyliczyć oceny EUMNK(FGLS) parametrów czyli b^_W^
4. pokazać solverem, że to oceny b^_W^ minimalizują uogólnioną sumę kwadratów reszt (jako punkty startowe można przyjąć zmyślone liczby lub oceny zwykłej MNK)
5. wyliczyć V^_as(b^_W^) oraz V^(b^) i porównać błędy średnie b^_W^ oraz b^ czyli EUMNK i MNK
6. porównać oceny macierzy kowariancji i błędy średnie szacunku b^ w UMRL i w KMRL (czyli prawdziwe i fałszywe błędy średnie zwykłej MNK przy założeniu prawdziwości UMRL)
7. Porównać charakterystyki ekonomiczne (elastyczności, RTS i ich błędy śr. szacunku) w KMNRL i w UMNRL dla funkcji C-D
8. Potem proszę to samo zrobić z f. translog i porównać, jak uwzględnienie autokorelacji/heteroskedastyczności wpływa na przebieg RTS i elastyczności (to dla chętnych, ciekawych świata i chcących coś więcej z zaliczenia).
9. Powyżej można wedle uznania rozważać CD i translog statyczne lub dynamiczne jak kto chce.
10. Wyniki przedstawić w zgrabnych tabelkach lub na wykresach.

Pytanie do ćwiczenia: jak różnice w modelowaniu struktury stochastycznej (między KMNRL a UMNRL w wersjach z autokorelacją i heteroskedastycznością epsilon) wpływają na wnioskowanie o charakterystykach ekonomicznych funkcji produkcji? Wersja podstawowa: dla f. C-D; wersja dla zainteresowanych: dla funkcji translog.

UWAGA! Robiąc to można (radzę!!!!) wykorzystać dodatek MATRIX oraz funkcje dla W i W^-1 dla autokorelacji składników losowych opisane w dodatkach do excela – link ze strony zajęć. Są tam także funkcje W i W^-1 dla heteroskedastyczności, tylko proszę uważać na składnię – dobrze podać pierwszy argument!!

Wyniki dla sprawdzenia:

Autokorelacja:

dla statycznej f. C-D

	b^W^	D(b^W^)	b^	D(b^) umrl	D(b^) kmrl
b0	-3.41155	0.358668214	-3.9321	0.398482	0.237223
b1	0.469863	0.073073023	0.385068	0.081076	0.048056
b2	1.274956	0.124477674	1.448587	0.139544	0.08329

(zakładając j^=0.574605; (ze statystyki D-W); jak ktoś wziął inne j mogą być inne nieco wyniki.)

Dla dynamicznej C-D:

	b^W^	D(b^W^)	b^	D(b^) w umrl	D(b^) w kmrl
t	0.006009746	0.002684	0.005196	0.0029175	0.0022371
b0	-2.48953536	0.528287	-3.01247	0.6156646	0.4549047
b1	0.338597447	0.092583	0.293913	0.0971856	0.0599889
b2	1.198873214	0.12319	1.339572	0.1428711	0.0915742

(zakładając j^=0.585836)

Heteroskedastyczność:

dla statycznej f. C-D

	b^W^	D(b^W^)	b^	D(b^) umrl	D(b^) kmrl
b0	-3.34313	0.240891	-3.9321	0.28068	0.237223
b1	0.511921	0.036112	0.385068	0.048382	0.048056
b2	1.223711	0.073444	1.448587	0.092101	0.08329

(podział na podpróby: do 1946 i od 1947, s²₁/s²₂ = 6.048302471)

Dla dynamicznej C-D:

	b^W^	D(b^W^)	b^	D(b^) umrl	D(b^) kmrl
t	0.005543635	0.00266	0.005196	0.002822	0.0022371
b0	-2.482090724	0.513776	-3.01247	0.557322	0.4549047
b1	0.391457348	0.061093	0.293913	0.067879	0.0599889
b2	1.150606007	0.088592	1.339572	0.101602	0.0915742

(podział na podgrupy (heteroskedastyczność): do 1946 i od 1947, s²₁/s²₂ = 4.228041646)