Zajęcia 18
Łączna estymacja modelu SURE: estymator Zellnera
1.
Notacja,
cz. 1
W analizie modelu typu SURE bardzo ważne jest dokładne rozumienie notacji. Dużo tu osiągamy dzięki manipulowaniu zapisem, dlatego zostanie on dość dokładnie wyjaśniony. Ale trzeba bardzo uważać, co który symbol oznacza, bo będziemy sobie dorzucać indeksy z góry i dołu; proszę więc pilnie baczyć co jest co i jaki ma wymiar.
Rozważmy liniowy model wielorównaniowy złożony z n osobnych równań regresji. Każde równanie ma postać podobną jak w KMRL, czyli:
W takim układzie równań każde równanie ma swoiste zmienne objaśniane, swoiste zmienne objaśniające i swoiste parametry. Zakładamy dla uproszczenia, że w każdym równaniu jest tyle samo (T) obserwacji. Dla wszystkich T obserwacji można taki układ zapisać jako:
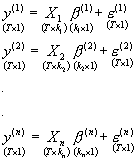
gdzie górny indeks w nawiasie (i) odpowiada numerowi równania (tylko w przypadku macierzy X indeks jest na dole i bez nawiasu – bo przy dużym X nie stosowaliśmy dotąd dolnego indeksu i nie ma się z czym pomylić). W i-tym równaniu jest ki zmiennych objaśniających i ki parametrów.
Powyżej układ ten jest zapisany dla wszystkich n równań i T obserwacji łącznie. Dla obserwacji o numerze t taki układ ma postać:
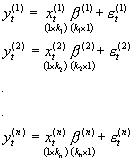
t
= 1,...,T.
Tutaj 
oznacza t-ty wiersz macierzy Xi.
Gdyby w powyższym zapisie zebrać równoczesne (odpowiadające temu samemu numerowi obserwacji, czyli temu samemu t) wartości y oraz e (czyli powyżej występujące jeden pod drugim y i e), otrzymalibyśmy dwa n-wymiarowe wektory. Na mocy konwencji wielkości równoczesne zapisujemy jako wiersze:
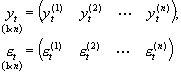
(podobny zapis w odniesieniu do y był już stosowany w przypadku liniowych modeli wielorównaniowych, tylko tam zmienne objaśniające (X) były takie same w każdym równaniu.
2.
Problem
w modelu SURE
Teraz można zapytać, jaki jest sens rozważania takiego modelu? I co wiąże te n równań, skoro mają osobne zmienne, osobne parametry i składniki losowe? Spróbujmy wyobrazić sobie przykład: rozważmy funkcje inwestycji (lub zysku, produkcji etc.) dla kilku dużych korporacji. Dla każdej firmy mamy T obserwacji z kolejnych lat, odpowiednie wartości zmiennych objaśniających itd. Parametry funkcji inwestycji (lub produkcji etc.) każdej firmy są indywidualne. Te funkcje możemy zebrać w układ równań odpowiadający opisywanemu modelowi. Co je łączy? Otóż modelowane przedsiębiorstwa działają w tym samym środowisku. Można więc oczekiwać, że bodźce z zewnątrz wpływają na nie w podobny sposób. Duże załamanie koniunktury w pewnym okresie odbije się na wszystkich firmach, podobnie boom gospodarczy itd. Oznacza to, że czynniki zakłócające, przypadkowe dla każdej firmy (każdego równania) nie są od siebie niezależne. Co to oznacza w kontekście struktury stochastycznej modelu? Żeby zbadać związek między składnikami losowymi różnych równań dla tej samej obserwacji, musimy rozważyć macierz kowariancji wektora równoczesnych składników losowych:
czyli:
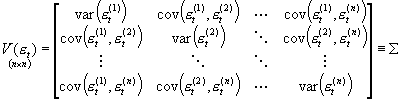
Jeżeli kowariancje pomiędzy składnikami losowymi różnych równań dla tego samego numeru obserwacji są niezerowe, to S, czyli macierz równoczesnych kowariancji składników losowych jest niediagonalna. Wtedy zależność pomiędzy pozornie niepowiązanymi równaniami kryje się w zależności ich równoczesnych składników losowych.
Uwaga! O składnikach losowych przyjmujemy tu standardowe założenia dla modeli wielorównaniowych (p
Zakładamy tu, że pomiędzy składnikami losowymi różnych obserwacji związek nie zachodzi! (niezależnie czy to składniki losowe tego samego równania czy różnych równań)
Rozważamy więc sytuację gdy:
dla i,
j = 1,2,...n
dla i, j
= 1,2,...n ORAZ t ¹ s.
Co jeszcze dodatkowo zakładamy? Spójrzmy na zapis:
dla t =
1,2,...,T
widać tu, że po prawej stronie nie występuje indeks t. Oznacza to, że dla każdego t macierz równoczesnych kowariancji składników losowych jest taka sama.
Podsumowując, chcemy modelować równania związane wyłącznie zależnością równoczesnych składników losowych – istotną rolę odgrywać będzie więc macierz równoczesnych kowariancji składników losowych S. Dla uproszczenia zakładamy, że zależność składników losowych w różnych okresach (jeśli t interpretujemy jako czas) nie występuje.
3.
Notacja,
cz. 2
Teraz główny pomysł w analizie systemów SURE jest taki, żeby opisany wyżej model wielorówaniowy zapisać w postaci jednorównaniowej, i do niej stosować wszystkie znane już metody. Robi się to następująco: wszystkie wektory y(i) ustawia się jeden pod drugim tworząc jeden długi wektor; podobnie postępujemy z wektorami składników losowych. Analogicznie tworzymy długi wektor nieznanych parametrów złożony z ustawionych jeden pod drugim wektorów b(i); macierze Xi poszczególnych równań grupujemy w jednej macierzy blokami na głównej przekątnej (struktura blokowo-diagonalna). Powstałe w ten sposób wektory i macierz oznaczamy „falą”:
;
;
;
;
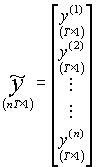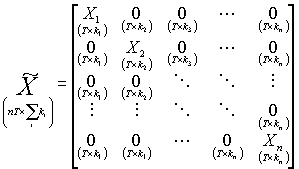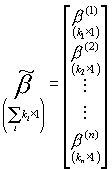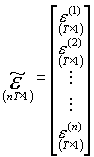Wtedy zapis:
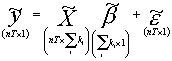
definiuje model jednorównaniowy dla nT obserwacji, ale równoważny z rozpatrywanym na początku układem n równań po T obserwacji każde. Można prześledzić, jak odpowiednia struktura macierzy „z falą” sprawia, że modele te sobie odpowiadają.
Dla
wnioskowania w tak zdefiniowanym modelu jednorówaniowym kluczowe znaczenie ma
pytanie: jaka jest postać macierzy kowariancji 
? Innymi słowy, jak struktura układu n równań z
niediagonalną macierzą równoczesnych kowariancji S przekłada się na
strukturę macierzy kowariancji złożonego długiego wektora składników losowych w
przekształconym modelu jednorównaniowym? Jej ustalenie sprowadziłoby taki model
do znanej nam postaci zgodnej z UMRL, moglibyśmy zastosować estymator Aitkena
(UMNK/EUMNK) – na tym polega procedura Zellnera estymacji modeli SURE.
4.
Estymator
Zellnera
W wyjściowym
układzie n równań występowały kowariancje między składnikami losowymi
równań o tym samym numerze obserwacji. Aby ustalić strukturę 
, musimy się zastanowić, gdzie w niej znajdą się epsilony
odpowiadające temu samemu t. Wynika to z konstrukcji wektora 
; w nim wektory (T ´ 1) składników losowych
każdego z n równań e(i) ułożone są jeden pod drugim.
Macierz 
ma wymiary nT ´ nT.
Jej pierwszy blok o wymiarach T ´ T to macierz
kowariancji e(1).
Pod nim będzie kolejny blok T ´ T zawierający
kowariancje między wektorem e(1)a e(2) itd. W
ten sposób macierz 
będzie się składać z n2
bloków o wymiarach T ´ T, przy czym i,j-ty blok będzie
zawierał kowariancje między wektorami e(i)a
e(j).
Jaką strukturę będzie mieć każdy z tych bloków? Kowariancje odpowiadające
różnym numerom obserwacji (czyli leżące poza przekątną bloku) będą zerowe; na
przekątnej będzie kowariancja składników losowych i-tego oraz j-tego
równania, czyli i,j-ty element z macierzy S. Jak matematycznie
opisać taką strukturę? Bardzo pomocny jest w tym tzw. iloczyn Kroneckera (ozn. Ä)– omówiony
dokładniej w innym miejscu, posiadający wiele przydatnych własności. Oznaczmy
macierz kowariancji 
przez W;
wtedy:
.
Zauważmy, że
nie wyprowadzamy tu przed macierz W czynnika skalującego s2 – byłby on nieidendyfikowalny;
macierz W
zawiera tylko elementy S lub zera (nie ma w niej np. jedynek) ; ponieważ
elementy S
są nieznane i będą podlegać estymacji, skalar s2 byłby
nieidentyfikowalny – istniałoby nieskończenie wiele kombinacji wartości s2
oraz S
równoważnych obserwacyjnie – odpowiadających takiej samej macierzy 
.
Teraz do estymacji wektora
parametrów 
możemy zastosować
estymator Aitkena; uwzględniając postać 
otrzymujemy:
,
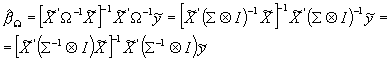gdzie ostatnia równość wykorzystuje własności iloczynu Kroneckera (AÄB)-1 = A-1ÄB-1.
Asymptotyczna macierz kowariancji tego estymatora ma postać:
Aby zastosować omawiany estymator parametrów strukturalnych (czyli przejść od UMNK do EUMNK) potrzebujemy jeszcze estymatora nieznanych parametrów struktury stochastycznej, czyli macierzy S równoczesnych kowariancji. Aby go otrzymać wykorzystamy (jak zwykle) reszty MNK.
Estymator macierzy S oznaczmy przez S; typowy element macierzy S to:
,
gdzie 
wektor (T ´ 1)
reszt MNK z i-tego równania układu SURE. Aby dogodnie numerycznie
otrzymać macierz S, najlepiej zgrupować wektory (T ´ 1)
reszt MNK poszczególnych n równań jeden obok drugiego, tworząc macierz E
(T ´
n):
; wtedy: 
Reszty MNK (ale zgrupowane w jeden długi wektor) można otrzymać jako:
Ostatecznie estymator parametrów strukturalnych systemu SURE metody Zellnera jest dany jako:
,
a zgodny estymator jego asymptotycznej macierzy kowariancji to:
- z elementów przekątniowych ostatniej macierzy uzyskujemy przybliżone błędy średnie szacunku ocen parametrów strukturalnych.
5.
Szczególne
przypadki estymatora Zellnera
W pewnych szczególnych przypadkach estymator metody Zellnera jest równoważny estymatorowi zwykłej MNK stosowanej osobno dla każdego równania (lub łącznie dla dużego układu „z falą”). Jeden przypadek jest intuicyjnie oczywisty: gdy S jest macierzą diagonalną, równoczesne kowariancje składników losowych różnych równań są zerowe, więc nie występuje efekt SURE – między równaniami nie ma wtedy żadnego związku.
Drugi przypadek jest nieco mniej oczywisty – ma on miejsce wtedy, gdy zmienne objaśniające poszczególnych równań są takie same (czyli Xi = X* dla i = 1,2,...,n). Wtedy również estymator Zellnera sprowadza się do estymatora MNK równanie po równaniu. Poniżej przedstawimy wyprowadzenie tej ostatniej własności.
Gdy macierz Xi każdego równania jest taka sama (równa X*), to:
Wtedy:
[powyżej
wykorzystujemy własność transpozycji iloczynu Kroneckera (AÄB)’ = (A’ÄB’)]
[korzystając z (AÄB)(CÄD) = ACÄBD]
[korzystając z (AÄB)-1 = A-1ÄB-1 oraz (AÄB)(CÄD) = ACÄBD]
co po uwzględnieniu struktury
wektora 
sprowadza się do:
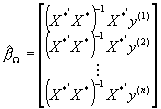
czyli estymatora zwykłej MNK równanie po równaniu - niezależnie od prawdziwej postaci S.
Omawiany tu przypadek identycznych zmiennych objaśniających odpowiada postaci URF (zredukowanej bez restrykcji) liniowego modelu wielorównaniowego Y=XP+V (tylko że tu zapis nie jest „kroneckerowski”, co jest możliwe, ponieważ X są wspólne) – uzasadnia to szacowanie URF zwykłą MNK.
Pokazaliśmy powyżej, jak manewrując zapisem sprowadzić układ n pozornie niezależnych równań do postaci umożliwiającej stosowanie estymatora Aitkena.
6.
Iterowany
estymator Zellnera
Opisana powyżej procedura przebiega następująco:
1. szacujemy równanie „z falą” zwykłą MNK, uzyskujemy reszty.
2. na podstawie reszt zw. MNK otrzymujemy macierz S czyli ocenę S
3. macierz S wykorzystujemy do b^W^ i uzyskujemy oceny parametrów
Zauważmy, że wykorzystując oceny parametrów z punktu 3 możemy uzyskać kolejne reszty (już nie MNK, tylko estymatora Zellnera); możemy na ich podstawie otrzymać kolejną ocenę macierzy S, potem znowu oceny parametrów, reszty, macierz S itd.
Taka iteracyjna procedura ma pewne interesujące własności teoretyczne. Dowodzi się mianowicie, że w granicy (po osiągnięciu zbieżności) oceny b i S iterowanego estymatora Zellnera są równoważne numerycznie ocenom z Metody Największej Wiarygodności.
Uzyskiwaniem ocen MNW parametrów SURE zajmiemy się w następnych zajęciach. Tu zaznaczmy tylko, że oceny MNW (czyli iterowanego estymatora Zellnera) mają takie same własności teoretyczne jak oceny uzyskane z estymatora Zellnera. Wartości liczbowe są oczywiście inne.
Problem jest taki, że zarówno jeśli chodzi o MNW, jak i estymator Zellnera, możemy ogólnie podać tylko własności dużej próby – asymptotyczne, i o obydwu tych estymatorach można powiedzieć z grubsza to samo. Ich zachowanie w małej próbie może być inne, ale to, który będzie lepszy, zależy od konkretnej próby, ogólnie nie można tu nic powiedzieć.
Estymator MNW pozwala nam na nieco więcej – można np. uzyskać błędy średnie szacunku elementów S, inaczej testować itd. Jednak jeśli jesteśmy zainteresowani wyłącznie ocenami parametrów b, to na gruncie teorii nie znajdujemy rozstrzygnięcia na rzecz jednego z estymatorów – decyzja to nasza sprawa J
Można jeszcze dodać, że z teoretycznego punktu widzenia to wszystko jedno, czy do konstrukcji S wykorzystamy reszty MNK i na tym poprzestaniemy, czy użyjemy reszt z estymatora Zellnera... teoria wymaga, by użyć reszt uzyskanych ze zgodnego estymatora b, a obydwa te estymatory są zgodne.
Przykład
empiryczny:
Model SURE dla funkcji inwestycji 5 amerykańskich korporacji na podstawie danych z 20 lat. Szczegóły są na stronie z danymi. Do implementacji przydaje się moduł matrix 1.5 ze strony dodatki to excela. Ponadto pomóc mogą umieszczone tam metody dla uzyskiwania iloczynu Kroneckera w Excelu.
Zadanie: na podstawie
omawianych danych:
- uzyskać oceny zwykłej MNK w modelu SURE
- uzyskać oceny estymatora Zellnera w modelu SURE
- uzyskać przybliżone błędy średnie szacunku ocen estymatora Zellnera
- przeprowadzić iterowany estymator Zellnera, uzyskując oceny b oraz S
Komentarz:
Uwaga: w przykładzie T = 20, n = 5
Zaczynamy od przyjęcia za S macierzy jednostkowej, robimy S-1 i konstruujemy macierz W^-1 = S-1 Ä I (to najciekawsza robota, bo ma 10000 elementów), potem wykorzystując ją robimy b^W^ . Nie mamy tylko co wstawić za S (bo jest tam na razie macierz jednostkowa). Odwołując się do parametrów b^W^ (które obecnie są ocenami zwykłe MNK, bo S=I) robimy reszty, ustawiamy je w macierz E jak opisano powyżej i tworzymy S = 1/T E’E. Uzyskane wartości „wklejamy specjalnie->wartości” za macierz jednostkową w miejscu S. Teraz trzeba tylko dostać V^as(b^W^), ale to po prostu kawałek formuły na b^W^ który trzeba wyciąć i wkleić w innym miejscu i tyle.
Dla iteracji estymatora Zellnera należy zrobić proste makro które będzie kopiować wartości S z reszt odpowiadających „bieżącym” ocenom parametrów b oraz je „wklejać specjalnie->wartości” w miejsce macierzy S wykorzystywanej do uzyskania ocen parametrów b. Może to brzmi niejasno, ale jest proste. JJ
Poniżej podaję wyniki dla sprawdzenia:
|
Zwykła MNK: oceny b |
Macierz S (ocena S) na podstawie reszt zwykłej MNK: |
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
Estymator Zellnera b^W^ z macierzą W^ wykorzystującą S z reszt MNK |
Macierz S (ocena S) na podstawie reszt uzyskanych z b^W^ (wartości obok) |
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
Iterowany estymator Zellnera dla b: |
Iterowany estymator Zellnera: macierz S: |
||||||||||||||||||||||||||||||||||||||||
|
|