Zajęcia 20

Modele SURE: estymacja MNW

1. Wstęp

Założenia Metody Największej Wiarygodności oraz własności uzyskanych przy jej pomocy estymatorów omówione zostały na wykładzie. Tu skupimy się na operacyjnej stronie estymacji MNW. Procedura estymacji metodą największej wiarygodności zostanie najpierw ogólnie zarysowana, a potem zastosowana do modelu spełniającego założenia UMNRL. Ogólnie przebiega ona następująco:

ustalamy rozkład obserwacji (y) w zależności od nieznanych parametrów.
rozpisujemy funkcję gęstości tego rozkładu
tworzymy funkcję wiarygodności, tj. reinterpretujemy funkcję gęstości z punktu 2: zamiast funkcji obserwacji (y) przy ustalonych parametrach, traktujemy ją jak funkcję nieznanych parametrów przy ustalonych wartościach obserwacji.
maksymalizujemy wartość funkcji wiarygodności względem jej argumentów (odpowiadających nieznanym parametrom wyjściowego modelu).
w celu znalezienia maksimum możemy poddawać funkcję wiarygodności wszelkim przekształceniom które nie zmieniają lokalizacji ekstremum a ułatwiają optymalizację
wartości argumentów maksymalizujące wartość funkcji wiarygodności to oceny MNW nieznanych parametrów

Intuicyjny sens takiego postępowania jest następujący: szukamy takich wartości parametrów, które - w ramach przyjętego modelu - maksymalizują prawdopodobieństwo pojawienia się rzeczywiście zaobserwowanych wartości y.

2. Rozkład obserwacji

Zgodnie z założeniami UMNRL, mechanizm powstawania obserwacji jest następujący:

X oraz b traktujemy jak wielkości nielosowe. Wektor e ma T-wymiarowy rozkład normalny o wartości oczekiwanej będącej wektorem zerowym oraz macierzy kowariancji W.

[nie rozpatrujemy tu oddzielnego czynnika skalującego macierz kowariancji składników losowych, czyli s². W niniejszych zajęciach zajmować się będziemy model SURE, w którym nie wyodrębnia się s²]

Można to zapisać następująco: . Jaki wobec tego rozkład ma y? Z własności wielowymiarowego rozkładu normalnego wynika, że liniowa transformacja zmiennej normalnej ma również rozkład normalny:

[ x~Nⁿ(m, S); gdy y = b + Ax, to y~N^m(Am+b, ASA’) ]

wobec tego y ma T-wymiarowy rozkład normalny o wartości oczekiwanej równej Xb i macierzy kowariancji W:

wobec tego prawdopodobieństwo pojawienia się obserwacji warunkowo względem ustalonych wartości parametrów b oraz W jest opisane następującą funkcją gęstości:

Zapis: oznacza funkcję gęstości T-wymiarowego rozkładu normalnego o wartości oczekiwanej m i macierzy kowariancji S.

3. Funkcja wiarygodności

W tym miejscu zmieniamy „optykę”: ustalamy y - staje on się niezmiennym parametrem funkcji, natomiast nieznane elementy b oraz W traktujemy jak zmienne – argumenty funkcji.

UWAGA! kiedy przechodzimy na funkcję wiarygodności, b oraz W i inne dotychczasowe parametry nie są już „nieznanymi stałymi”, stają się natomiast zmiennymi – argumentami po których będziemy prowadzić optymalizację. Zamiast patrzyć na nie jak na oznaczenia nieznanych wartości, zastanawiamy się, co należałoby za nie podstawić, aby zmaksymalizować wartość funkcji.

Tą zmianę zaznaczamy następująco: y – jako wielkość ustaloną – przesuwamy w nawiasie na prawo i oddzielamy średnikiem, natomiast argumenty – na lewo. Funkcję wiarygodności oznaczamy przez L od likelihood. Ostatecznie:

Wartości nieznanych elementów b oraz W maksymalizujące L(b, W; y) są szukanymi ocenami MNW tych parametrów. Maksymalizację możemy w niektórych przypadkach przeprowadzić całkowicie lub częściowo metodami analitycznymi. Zwykle jednak po niektórych parametrach trzeba będzie prowadzić optymalizację metodami numerycznymi. Ważne jest, by starać się zredukować wymiar i złożoność problemu numerycznego.

W tym celu zwykle logarytmuje się funkcję wiarygodności, otrzymując tzw. log-likelihood function, oznaczaną przez l (małe L):

Możemy zamiast L rozpatrywać równoważnie jej logarytm, ponieważ ln() – będąc przekształceniem monotonicznym – nie zmienia lokalizacji ekstremum.

Oceny MNW uzyskujemy następująco:

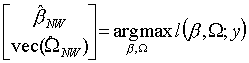
(vec(W) oznacza, że nieznane elementy W ułożone są w wektor-kolumnę, aby uzyskać spójność zapisu; w dalszym ciągu operator wektoryzacji macierzy zostanie pominięty)

4. Koncentracja funkcji wiarygodności: idea, notacja.

Zastanówmy się, czy możemy w tym miejscu jeszcze jakoś uprościć postać funkcji l. Możemy w celu maksymalizacji pominąć wszystkie stałe, tj. składniki niezależne od b oraz W. To jednak uprości problem bardzo nieznacznie.

Szukamy argumentu maksymalizującego l po b, W. Czy pomogłoby nam, gdybyśmy wiedzieli, jakie b maksymalizuje funkcję wiarygodności warunkowo względem dowolnych ustalonych wartości W? Innymi słowy, czy przydatna byłaby znajomość funkcji analitycznego ekstremum warunkowego?

[dlaczego „funkcji”? bo wartości b maksymalizujące L przy dowolnej ustalonej wartości W muszą zależeć właśnie od wartości W. Czyli takie ekstremum warunkowe to funkcja do której wysyłamy W a zwraca nam b ]

Gdyby taką funkcję ekstremum warunkowego podstawić do funkcji wiarygodności wszędzie w miejsce b, wartość L zależałaby wyłącznie od nieznanych elementów W. Pozwoliłoby to znacznie zmniejszyć wymiar problemu, ponieważ numeryczną optymalizację trzeba by było prowadzić wyłącznie po elementach W.

Takie postępowanie to koncentracja funkcji wiarygodności. Oczywiście potencjalnie można ją przeprowadzić „w drugą stronę” – mając odpowiednie ekstremum warunkowe podstawić za W i maksymalizować po b.

Formalnie maksymalizację z wykorzystaniem koncentracji można zapisać jako:

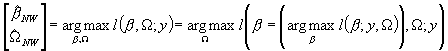
Jeszcze inny zapis mógłby wyglądać tak:

;

podkreśla on fakt, że wartości b warunkowo maksymalizujące logarytm funkcji wiarygodności są funkcją W. Wtedy:

1) Koncentracja l po b polega na podstawieniu do l - w miejsce b - funkcji . Uzyskujemy wtedy skoncentrowaną funkcję wiarygodności (ozn. l*), której argumentem są wyłącznie nieznane elementy W; i tylko po nich musimy przeprowadzić numeryczną maksymalizację.

;

oceny MNW parametrów uzyskujemy jako:

(numerycznie)

(analitycznie)

2) Koncentracja l po W polega na podstawieniu do l - w miejsce W - funkcji . Uzyskujemy wtedy skoncentrowaną funkcję wiarygodności l*, której argumentem są wyłącznie nieznane elementy b; i tylko po nich musimy przeprowadzić numeryczną maksymalizację.

;

oceny MNW parametrów uzyskujemy jako:

(numerycznie)

(analitycznie)

Aby przeprowadzić koncentrację funkcji wiarygodności, trzeba oczywiście znać konkretną postać odpowiednich analitycznych funkcji maksimum warunkowego. Poniżej przedstawiona zostanie funkcja wiarygodności dla modelu SURE oraz odpowiednie maksima warunkowe pozwalające przeprowadzić jej koncentrację.

5. Funkcja wiarygodności w modelu SURE

W modelu SURE (por. zajęcia 19) doprowadzamy model wielorównaniowy do postaci jednorównaniowej, a następnie stosujemy w tak przekształconym modelu estymator Aitkena. W takim modelu macierz kowariancji składników losowych jest dana jako :W = SÄI (przy czym W^-1 = S^-1ÄI).

UWAGA! w zajęciach 19 mieliśmy wektor y (o długości nT, więc rozkład obserwacji będzie nT-wymiarowy), blokowo-diagonalną macierz X oraz długi wektor parametrów oznaczone były falą. Tutaj rezygnujemy z tego oznaczenia; wektory i macierze pozbawione dolnych czy górnych indeksów domyślnie są „z falą”, natomiast wszystkie inne oznaczamy tak, jak w zajęciach 19.

Logarytm funkcji wiarygodności dla SURE będzie miał więc postać:

z własności iloczynu Kroneckera [det(AÄB)=det(Aⁿ)det(B^m) macierz A jest m´m, B n´n]:

ostatecznie więc:

aby przeprowadzić koncentrację takiej funkcji, musimy znać postaci odpowiednich ekstremów warunkowych.

6. Warunkowa maksymalizacja funkcji wiarygodności

W celu wyprowadzenia postaci warunkowego ekstremum względem elementów b, wyjedziemy od specyfikacji odpowiadającej UMNRL, tzn. z macierzą kowariancji składników losowych równą W (zamiast szczególnej postaci :W = SÄI). Aby znaleźć zastanówmy się, który element l(b, W; y) zależy od b. Tym elementem jest . Zauważmy, że sprowadza się to do pewnej formy kwadratowej wziętej ze znakiem minus. Wobec tego wartość b minimalizująca tę formę, maksymalizuje funkcję wiarygodności. Widać, że rozważana forma kwadratowa odpowiada uogólnionej sumie kwadratów reszt z UMRL. W zajęciach 18 pokazaliśmy, że to estymator Aitkena b^_W minimalizuje uogólnioną sumę kwadratów reszt. Jest więc on – jako funkcja W – szukaną funkcją ekstremum warunkowego . Poniżej udowodnimy jednak innym sposobem, że minimalizuje po b funkcję .

Rozważmy najpierw warunkową maksymalizację logarytmu funkcji wiarygodności po elementach wektora b. Jak pokazaliśmy sprowadza się to do minimalizacji po b następującej formy kwadratowej:

(wychodzimy od prostego przekształcenia formy kwadratowej: do wektorów z obydwu stron dodajemy i odejmujemy Xb^_W , co nie zmienia ich wartości)

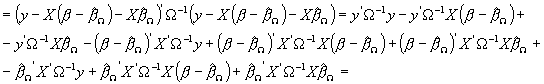
(pozbywamy się nawiasów wykonując wszystkie operacje mnożenia)

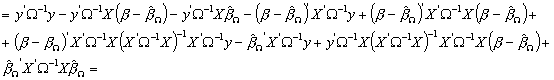
(podstawiamy w niektórych składnikach, co pozwoli je skrócić

otrzymując ostatecznie:)

w tym wyrażeniu jedynie trzeci składnik – kolejna forma kwadratowa – zależy od b, wystarczy więc znaleźć taką wartość b która zminimalizuje tę formę kwadratową. Jest to forma kwadratowa wykorzystująca macierz dodatnio określoną [jeśli W jest (jako macierz kowariancji) dodatnio określona, to jej odwrotność także] Z definicji dodatniej określoności wynika, że odpowiednia forma kwadratowa dla dowolnego wektora [tu ] (z wyjątkiem wektora zerowego) może przyjmować jedynie wartości nieujemne. Wobec tego ma ona swoje minimum gdy odpowiedni wektor jest równy zero, czyli gdy zachodzi , z czego wynika . Oznacza to, że aby zmaksymalizować funkcję wiarygodności względem b, należy za b podstawić estymator Aitkena (rozumiany jako funkcja W). Dla modelu SURE skorzystamy z konkretnej postaci macierzy W uzyskując:

Warunkowa maksymalizacja logarytmu funkcji wiarygodności po elementach W (czyli dla SURE po elementach S) jest trudniejsza, więc przedstawimy tu jedynie jej wynik. Zauważmy przedtem tylko, że funkcja warunkowego maksimum dla elementów b odpowiadała stosowanemu w procedurze Zellnera estymatorowi wektora b. Okazuje się, że funkcja warunkowego ekstremum po elementach S odpowiada opisanemu w zajęciach 19 estymatorowi macierzy S, czyli macierzy S o typowych elementach:

alternatywny wzór wymagał ułożenia reszt poszczególnych równań kolumnami obok siebie:

; wtedy:

Oczywiście żeby traktować S jako funkcję warunkowego ekstremum, musi ona zależeć od b. Dlatego we wzorach powyżej nie oznacza reszt MNK, tylko funkcję b, tj. reszty wynikające z przyjęcia konkretnej wartości b. Otrzymujemy więc:

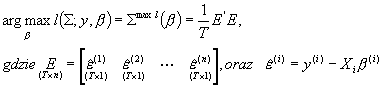
Skoro znamy już postać odpowiednich funkcji warunkowych maksimów, możemy przystąpić do koncentracji funkcji wiarygodności dwoma alternatywnymi sposobami:

7. Skoncentrowana funkcja wiarygodności dla SURE; cz. 1: Koncentracja po b.

Przypomnijmy postać logarytmu funkcji wiarygodności modelu SURE:

po koncentracji uzyskujemy:

W celu uzyskania ocen MNW nieznanych parametrów należy numerycznie zmaksymalizować daną powyżej funkcję względem nieznanych elementów macierzy S. Macierz ta (jako macierz kowariancji) jest symetryczna stopnia n, zawiera więc (n²- n) / 2 + n nieznanych elementów.

Jednak to nie wszystko co wiemy o macierzy S. Musi być ona macierzą dodatnio określoną. Musimy ten warunek uwzględnić w estymacji. Jest to konieczne choćby dlatego, że jeśli algorytm numeryczny „wjedzie” przypadkowo w obszar przestrzeni parametrów gdzie S jest niedodatnio określona, jej wyznacznik będzie niedodatni więc jego logarytm (pojawiający się w l*) spowoduje wystąpienie błędu numerycznego.

Poradzić sobie z tym problemem można na dwa sposoby:

Po pierwsze, można spróbować maksymalizacji z ograniczeniami. Trzeba wtedy skonstruować odpowiednią funkcję-kryterium ograniczające, która będzie „pilnowała” dodatniej określoności S. Spakietowane w programach algorytmy numeryczne zwykle pozwalają na dodanie ograniczenia właśnie poprzez specjalną funkcję, której wartość ma być np. większa od zera zawsze gdy żądana restrykcja jest spełniona. W przypadku rozważanej tu restrykcji dodatniej określoności macierzy, najwygodniej jest skorzystać z kryterium opartego na jej wartościach własnych. Wartości własne macierzy symetrycznej są zawsze rzeczywiste; warunek konieczny i wystarczający dodatniej określoności macierzy to dodatniość wszystkich jej wartości własnych. Jest ich tyle, ile wynosi stopień macierzy. Wystarczy więc „pilnować” dodatniości najmniejszej wartości własnej. Alternatywne (równoważne) kryterium dodatniej określoności to kryterium wyznacznikowe; jego implementacja wymaga zwykle więcej zachodu (trzeba się pozastanawiać co to są wiodące minory główne J - jest ono za to szybsze numerycznie, bo wyznaczniki wylicza się prościej niż wartości własne, ale to komputer liczy). Podsumowując problem sprawdzania określoności macierzy symetrycznych: można skorzystać z kryterium wartości własnych (patrz zajęcia 16 punkt stabilność modelu), lub z kryterium wyznacznikowego, o którym parę słów postaram się jeszcze napisać.

Jest jednak drugi sposób poradzenia sobie z problemem dodatniej określoności S. Zauważmy, że sposób poprzedni – optymalizacji z ograniczeniami – może być bardzo nieefektywny, ponieważ restrykcje określoności mogą ucinać przestrzeń parametrów w bardzo skomplikowany sposób utrudniając życie algorytmowi numerycznemu. Możemy więc spróbować reparametryzować problem. Przejdziemy na nowe parametry (oznaczmy je przez l - to one będą w Solverze jako „Komórki zmieniane”) i wyrazimy elementy S poprzez ich funkcje. Te funkcje dobierzemy tak sprytnie, że

1) dla dowolnych wartości l macierz S będzie dodatnio określona

2) każdą dodatnio określoną macierz S można będzie wyrazić przez pewne wartości l

w ten sposób przenosimy się z optymalizacją w przestrzeń parametrów l, która nie jest ucięta żadnymi restrykcjami, zachowując możliwość wyrażenia wszystkich interesujących nas macierzy S.

Omawiane przekształcenie zaproponował Lawrence J. Lau w artykule Testing and imposing monoticity, convexity and quasi-convexity constraints. (jak kogoś interesuje, mogę podesłać)

Proponuje on wykorzystanie tzw. dekompozycji Cholesky’ego (Cholesky factorization). W skrócie idzie to tak:

Każdą dodatnio określoną macierz A można przedstawić w postaci: A = LDL’, gdzie:

L jest macierzą jednostkową trójkątną dolną, czyli: ma jedynki na przekątnej i zera ponad przekątną

D jest macierzą diagonalną (ma zera poza przekątną).

Warunkiem koniecznym i wystarczającym dodatniej określoności A jest, by wszystkie elementy na przekątnej D były dodatnie. Robimy więc tak: z wektora parametrów l po których puszczamy Solver nie robimy bezpośrednio S, tylko odpowiednio swobodne elementy macierzy L (pod przekątną) oraz D. D robimy w specjalny sposób – na przekątnej umieszczamy funkcję exp( ) wyjściowych parametrów l. W ten sposób diagonalne elementy D będą dodanie dla dowolnych wartości l. Za S podstawiamy LDL’, co zapewni jej dodatnią określoność dla dowolnych wartości parametrów. Jeżeli za punkt startowy przyjmiemy wektor zerowy, będzie to odpowiadało jednostkowej macierzy S. W taki sprytny sposób obeszliśmy problem skomplikowanych restrykcji matematycznych robiących bałagan w przestrzeni parametrów – solver chodzi po pomocniczych parametrach l które należą do R^k.

8. Skoncentrowana funkcja wiarygodności dla SURE; cz. 2: Koncentracja po S.

Koncentracja po S - w przeciwieństwie do koncentracji po b - nie będzie nastręczać problemów numerycznych. Za to analityczne wyprowadzenie postaci skoncentrowanej funkcji wiarygodności nie jest trywialne. Przebiega ono tak:

Zaczynamy od wyjściowej postaci logarytmu funkcji wiarygodności:, jednak przedstawimy ją inaczej niż dotychczas. Pamiętajmy, że funkcja wiarygodności powstaje z gęstości łącznego rozkładu obserwacji. Jak on wygląda w przypadku modelu SURE? Składniki losowe różnych okresów są nieskorelowane (ich kowariancje wynoszą zero). Wobec tego także obserwacje z różnych okresów są nieskorelowane, a ponieważ mają rozkład normalny, to i niezależne. Dla niezależnych zmiennych losowych łączna gęstość jest po prostu iloczynem gęstości brzegowych. Aby więc uzyskać łączny rozkład wszystkich obserwacji musimy wziąć rozkłady dla każdego t i zapisać ich iloczyn.

Jaki jest w modelu SURE rozkład obserwacji dla ustalonego pojedynczego t? dla konkretnego numeru obserwacji mamy n równań, n wartości y, więc i n-wymiarowy rozkład normalny. O jakich parametrach?

Przypomnijmy z zajęć 19 zapis układu SURE dla ustalonego t:

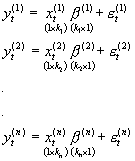, gdzie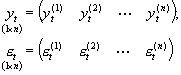

można to krócej zapisać jako:

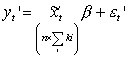
gdzie ma strukturę taką, jak miałby gdyby T wynosiło 1 (czyli ma strukturę blokowo-diagonalną, typowym i-tym blokiem przekątniowym jest t-ty wiersz z macierzy X_i.

Uwaga! Tu pojawiają się nam niespodziewanie transpozycje, ponieważ ustaliliśmy, że wartości równoczesne y oraz e są w wektorach-wierszach, dlatego proszę poniżej uważać, co jest wierszem a co kolumną.

Po tych manewrach notacyjnych możemy wreszcie powiedzieć, że rozkład pojedynczej obserwacji (czyli dla ustalonego t, czyli wektora y_t) to: n-wymiarowy rozkład normalny o wartości oczekiwanej i macierzy kowariancji S:

Łączny rozkład wszystkich obserwacji to iloczyn T takich rozkładów, co po zlogarytmowaniu daje funkcję wiarygodności o postaci:

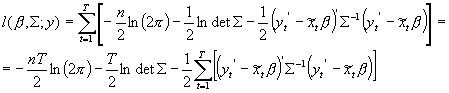
Poddajmy pewnym wyrafinowanym manipulacjom ostatni składnik funkcji wiarygodności; będziemy tu korzystać z własności śladu macierzy. Ślad (ozn. tr()) to suma elementów na głównej przekątnej.

(rozważana suma jest skalarem, ślad macierzy 1 na 1 to ona sama, więc do skalara możemy bezkarnie przyłożyć operator tr() )

(ślad sumy macierzy to suma śladów tych macierzy i vice versa, więc możemy zamieniać operatory śladu i sumy;

ponadto ślad iloczynu macierzy permutowanych cyklicznie jest taki sam, czyli tr(ABC) = tr(CAB) = tr(BCA) – możemy wziąć macierz z końca i dać na początek lub odwrotnie, ale bez zaburzania kolejności)

(tutaj znowu zamieniamy ślad z sumą, a następnie wyciągamy przed sumę S^-1, która nie zależy od t.

Zauważmy, że suma to dokładnie to samo, co iloczyn macierzy E’E zdefiniowanych wcześniej przy warunkowym maksimum po elementach S. (to łatwo zobaczyć, tylko trzeba sobie uświadomić, do to jest , a co . Oczywiście – tak jak poprzednio – wszędzie tu to nie reszty MNK, tylko funkcja konkretnej wartości b, co można by zapisać jako , czego nie robimy J. Ostatecznie więc

Skoro jednak mamy przeprowadzić koncentrację funkcji wiarygodności po S, to zgodnie z tym, co napisano wyżej, za S wstawimy S. Wtedy:

(oczywiście powyżej w obydwu wypadkach macierz S nie jest konkretną wartością, tylko funkcją parametrów b, jednak okazuje się, że element funkcji wiarygodności przed koncentracją wraz z postacią ekstremum warunkowego wzajemnie tworzą stałą funkcję parametrów b równą zawsze nT )

Ostatecznie więc skoncentrowana funkcja wiarygodności ma tu postać:

Oczywiście pamiętamy, że S jest funkcją reszt czyli funkcją b, co w ostatnim przejściu nie jest explicite zapisane.

Widać więc, że przy koncentracji po S, estymacja MNW będzie się sprowadzać do numerycznego znalezienia takich wartości parametrów, dla których wyznacznik prostej macierzowej funkcji reszt jest jak najmniejszy. Ponieważ wymaga to wyłącznie wyliczenia reszt oraz wyznacznika a na parametry nie nakładamy żadnych restrykcji, z punktu widzenia realizacji numerycznej, zagadnienie jest względnie proste.

Błędy średnie szacunku parametrów:

Przybliżone błędy średnie szacunku parametrów można uzyskać jako pierwiastki kwadratowe z oszacowania asymptotycznej macierzy kowariancji estymatora MNW stosując następujące wzory:

Zadanie:

Oszacować model SURE z zajęć 18 za pomocą MNW dwoma sposobami: raz z koncentracją po S, raz z koncentracją po b. Podać przybliżone błędy średnie szacunku ocen MNW b oraz S.

Jak to zrobić?

Zastosować wszystko co napisano powyżej J czyli: zakodować (razy dwa): skoncentrowaną funkcję wiarygodności, komórki po których będzie „chodził” solver – i to od nich oczywiście funkcja wiarygodności ma zależeć. Te komórki ustawiamy jako „komórki zmieniane” (raz będą to elementy b, a raz pomocnicze l z których robimy S), komórka z wartością skoncentrowanej funkcji wiarygodności to „komórka celu”; ponadto w Solverze zaznaczamy maksymalizację, wchodzimy do „Opcji” i tam: podnosimy czas i liczbę iteracji do 1000, gradienty przestawiamy na „Centralne”, „Dokładność”, „Tolerancję” „Zbieżność” ustawiamy na 1e-20.

Koncentracja po S jest prosta w realizacji – nie powinno być problemów. Koncentracja po b wymaga zastosowania opisanej powyżej reparametryzacji dla zapewnienia dodatniej określoności macierzy S – wtedy solver „chodzi” po parametrach pomocniczych l z których robimy macierze D oraz L a następnie S=LDL’ – i ta S dopiero wchodzi do funkcji wiarygodności. Dodatkowo – jest tam potrzebny iloczyn Kroneckera S^-1ÄI, który nie może być robiony funkcją Kron z „Dodatków do Excela” bo to będzie zbyt powoli działać. Strukturę S^-1ÄI trzeba zrobić specjalnym makrem (patrz: „Dodatki do Excela”). Oczywiście S^-1 musi być odwrotnością S zrobionej jako LDL’.

Iloczyn Kroneckera występujący we wzorze na oszacowanie macierzy kowariancji S^_NW można zrobić funkcją Kron z „Dodatków do Excela”. Dodatkowo dla łatwiejszego wyliczenia pierwiastków z elementów przekątniowych oszacowanej macierzy kowariancji estymatora można użyć funkcji diag_(.) z tego samego źródła.

W rozważanym przykładzie SURE jako oceny MNW (przy obydwu sposobach koncentracji) powinni Państwo uzyskać wartości parametrów odpowiadające iterowanemu estymatorowi Zellnera podanymi w zajęciach 19. Wartość logarytmu funkcji wiarygodności to –459.092225 (uwzględniając stałe). Jeżeli oceny parametrów są takie same (po zmaksymalizowaniu) a wartość funkcji inna, to pomylili się Państwo o stałą w skoncentrowanej funkcji wiarygodności.