Zajęcia 21

Estymacja MNW modeli jednorównaniowych

0. Wstęp

W niniejszych zajęciach podejmiemy próbę usystematyzowania wiadomości o estymacji modeli jednorównaniowych przy pomocy metody największej wiarygodności. W tym celu wprowadzimy dwa kryteria podziału:

A) Podział na modele:

-liniowe: y = Xb + e

-nieliniowe: y = g(X;b) + e

B) Podział na modele:

-o prostej strukturze stochastycznej: V(e) = s²I.

-o złożonej strukturze stochastycznej: V(e) = s²W.

Na potrzeby estymacji MNW zakładamy oczywiście, że składniki losowe e mają T-wymiarowy rozkład normalny, a także, że zmienne w macierzy X możemy traktować jakby były nielosowe. Różnice dotyczą w przypadku A) – postaci zależności strukturalnej między parametrami a zmiennymi objaśniającymi; w przypadku B) – postaci macierzy kowariancji składników losowych V(e). W ramach każdego podziału przypadek drugi jest ogólniejszy.

Rozpatrzymy poniżej kolejno cztery przypadki wynikające z różnych kombinacji kryteriów A i B:

I. -modele nieliniowe o złożonej strukturze stochastycznej: y = g(X;b) + e oraz V(e) = s²W.

(co odpowiada założeniom Modelu Uogólnionej Normalnej Regresji Nieliniowej – MUNRN)

II. modele liniowe o złożonej strukturze stochastycznej: y = Xb + e oraz V(e) = s²W.

(co odpowiada założeniom Uogólnionego Modelu Normalnej Regresji Liniowej – UMNRL)

III. modele nieliniowe o prostej strukturze stochastycznej: y = g(X;b) + e oraz V(e) = s²I.

(co odpowiada założeniom Modelu Normalnej Regresji Nieliniowej – MNRN)

IV. modele liniowe o prostej strukturze stochastycznej: y = Xb + e oraz V(e) = s²I.

(co odpowiada założeniom Klasycznego Modelu Normalnej Regresji Liniowej – KMNRL)

Najbardziej ogólne warunki opisuje oczywiście punkt I – model nieliniowy o złożonej strukturze stochastycznej; pozostałe punkty są jego szczególnymi przypadkami. Warto je jednak rozpatrywać, ponieważ w mniej ogólnych modelach (czyli przy silniejszych założeniach) da się uzyskać silniejszą tezę. W przypadkach III oraz IV uzyskamy nową – głębszą – interpretację znanych już Państwu wyników. Przypadki I oraz II stanowią pewną nowość.

Dla ilustracji wykorzystane zostaną funkcje produkcji translog (liniowa) oraz CES (nieliniowa); jako przykład złożonej struktury stochastycznej użyta będzie macierz W odpowiadająca autokorelacji typu AR(1) dla składników losowych (patrz zajęcia 17).

Przyjmujemy W = W(j) – co nie wszędzie poniżej jest explicite zaznaczone; wobec tego nieznane parametry modelu w przypadkach I oraz II to b,s²,j.

1. MUNRN – model nieliniowy ze złożoną strukturą stochastyczną

Rozważania rozpoczniemy od najbardziej ogólnego przypadku I – czyli modelu nieliniowego o złożonej strukturze stochastycznej, w którym:

oraz

gdzie g(X;b) jest (T´1) wektorem funkcji klasy C², oraz . Nieznane parametry modelu grupujemy w jeden wektor:

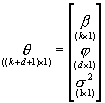
Przy czym zakładamy, że , czyli że pomiędzy parametrami b,s²,j nie ma zależności – zachodzi tzw. swobodna zmienność: wartości jakie przyjmują np. b nie mają wpływu na wartości jakie może przyjąć j.

Wobec tego rozkład obserwacji (wektora y) to T-wymiarowy rozkład normalny o wartości oczekiwanej g(X;b) i macierzy kowariancji s²W:

_.

PKP uprzejmie przypomina podróżnym, że cały czas W = W(j)

Funkcja wiarygodności ma w związku z tym następującą postać:

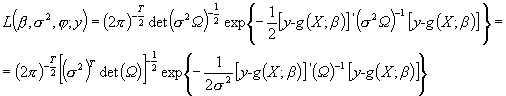
po zlogarytmowaniu otrzymujemy:

.

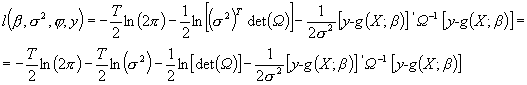Powyższą funkcję w ogólnym przypadku można skoncentrować tylko po s². W tym celu musimy znaleźć odpowiednie analityczne ekstremum warunkowe. Spróbujmy więc sprawdzić jaki jest warunek na zerowanie pochodnej cząstkowej l(b,s²,j.;y) względem s².

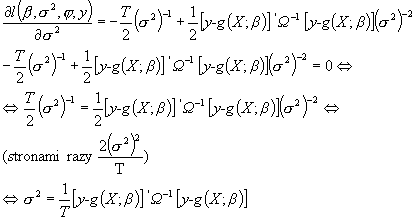
(można względnie łatwo stwierdzić, że także druga pochodna spełnia warunek istnienia maksimum w zadanym punkcie)

wobec tego analityczne maksimum warunkowe funkcji wiarygodności dla parametru s² ma postać:

;

możemy zauważyć, że znaleziona postać zawiera nieliniową uogólnioną sumę kwadratów reszt. Wykorzystując powyższą funkcję analitycznego maksimum warunkowego koncentrujemy logarytm funkcji wiarygodności po s² uzyskując:

(w ostatnim członie czynniki z oraz uproszczą się pozostawiając –T/2); ostatecznie:

.

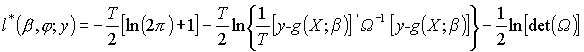(u Profesora może być na końcu +1/2 ln det V, ale to dlatego, że ; to na jedno wychodzi)

W przypadku przyjęcia dla W struktury wynikającej z autokorelacji AR(1) składnikówl losowych, można wykorzystać fakt, że: _.

Estymacja

Nieznane parametry modelu grupujemy w wektorze q:

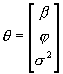
Aby oszacować MNW nieznane parametry modelu należy zadaną tak skoncentrowaną funkcję wiarygodności zmaksymalizować NUMERYCZNIE po elementach b oraz j uzyskując:

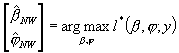
a następnie wykorzystując uzyskane wartości wyliczyć:

Przybliżone błędy średnie szacunku parametrów

Przybliżone błędy średnie szacunku parametrów uzyskamy jako pierwiastki z oszacowania asymptotycznej macierzy kowariancji estymatora MNW. Estymator asymptotycznej macierzy kowariancji uzyskujemy wykorzystując odwrotność macierzy informacyjnej Macierz informacyjną dzielimy na bloki odpowiadające podziałowi wektora q na b,j,s²:

;

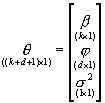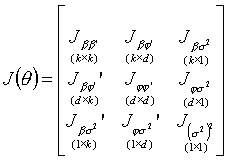
Macierz informacyjna jest symetryczna, więc odpowiednie bloki pod przekątną to transpozycje bloków nad przekątną. Przy pewnych założeniach macierz informacyjna ma strukturę blokowo-diagonalną – bloki oraz są zerowe. Dzięki temu możemy niezależnie odwracać bloki odpowiadające parametrom strukturalnym (b) lub parametrom struktury stochastycznej (s²,j) uzyskując:

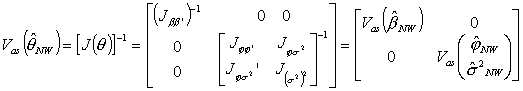
Ponieważ (jak Profesor pokazywał na wykładzie) blok to:

(tylko u Profesora bywa V, ale )

A(b) to macierz pierwszych pochodnych cząstkowych funkcji g(X;b) względem parametrów b. Jest to ta sama macierz która pojawiała się przy okazji MNRN i algorytmu Gaussa-Newtona w zajęciach 9:

W A(b) w wierszach są pochodne g(X;b) odpowiadających kolejnym wartościom x_t (T wierszy), a w kolumnach pochodne po kolejnych elementach wektora b - (k kolumn).

Wobec tego po odwróceniu przybliżone błędy średnie szacunku parametrów strukturalnych b uzyskujemy więc jako pierwiastki z elementów przekątniowych macierzy:

,

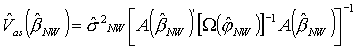która definiuje zgodny estymator .

Przybliżone błędy średnie szacunku parametrów struktury stochastycznej (j,s²)

(dla zainteresowanych)

Powyżej pokazano że:

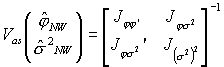
Profesor pokazywał, że:

;

postać pozostałych bloków zależy od przyjętej postaci funkcji W = W(j). Zgodnie ze wzorami podanymi na wykładzie:

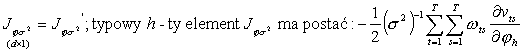
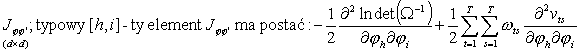
gdzie: v_ts to element [t,s] macierzy W^-1(j), a w_ts to element [t,s] macierzy W(j).

Jeżeli przyjmiemy postać W(j) odpowiadającą autokorelacji typu AR(1) dla składników losowych [opisaną w zajęciach 17], to korzystając z powyższych wzorów, można wyprowadzić postać odpowiednich bloków (będących skalarami, ponieważ wymiar j to w tym wypadku 1):

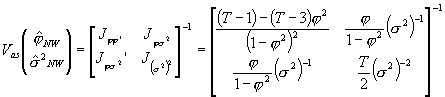
Co po podstawieniu za j oraz s² ocen MNW i odwróceniu pozwala uzyskać przybliżone błędy średnie szacunku tych parametrów jako pierwiastki kwadratowe z odpowiednich elementów powyższej macierzy. Aha, oczywiście ostatnią macierz powyżej można odwracać analitycznie – jeśli ktoś chce. Wtedy uzyskamy przybliżony błąd średni szacunku j (po uwzględnieniu pewnej aproksymacji – dla dużego T) wynoszący .

Wyprowadzenie wzoru na V_as(j^_NW s²^_NW)

(dla jeszcze bardziej zainteresowanych)

Profesor Podawał Państwu na wykładzie wyprowadzał wzory na poszczególne bloki macierzy informacyjnej w omawianym przypadku. Wyprowadzenie korzystało z faktu, że

gdzie E oznacza operator wartości oczekiwanej, zaś H[.] to hessian (macierz drugich pochodnych cząstkowych) zlogarytmowanej funkcji wiarygodności względem parametrów q. Uzyskane wzory na bloki oraz [podane powyżej] są „gotowe do użycia” – w ogólnym przypadku nic tu się nie da uprościć. Jeśli chodzi natomiast o bloki oraz , powyżej podana jest tylko ich ogólna postać oraz końcowy wynik dla szczególnego przypadku struktury AR(1) dla e. Aby „oswoić” Państwa z tematem, poniżej wzory te zostaną wyprowadzone. Pamiętajmy, że w przypadku rozważanej struktury j oraz blok są skalarne, więc nie ma potrzeby rozważania j_h czy j_i, tylko j.

Dla korzystamy ze wzoru: . v to element macierzy W^-1(j) (por. zajęcia 17). Musimy rozważyć sumę iloczynów (element W razy pochodna analogicznego elementu W^-1 po j ) – wobec tego wystarczy rozważać tylko te przypadki, gdzie element W^-1 jest funkcją j. Ze wzoru w zajęciach 17 widać, że jest tak w przypadku:

- elementów na głównej przekątnej W^-1 (bez pierwszego i ostatniego elementu - czyli pozostaje T-2 elementów) – tu pochodna po j wynosi 2j, oraz

- elementów na 2 sąsiednich przekątnych – jest ich 2 razy po T-1 – gdzie pochodna po j równa się –1.

Każdy z rozważanych elementów W^-1 z niezerową pochodną po j musimy przemnożyć przez odpowiedni element W. Otrzymujemy:

- z głównej przekątnej w sumie: (T-2)* [ 2j * 1/(1 - j²)^-1]

- z 2 sąsiednich przekątnych w sumie: 2(T-1)* [-1 * j/(1 - j²)^-1]

Ostatecznie , więc i o to chodziło.

Dla korzystamy ze wzoru: .

Rozważmy najpierw . Ponieważ , obliczmy pierwszą i drugą pochodną:

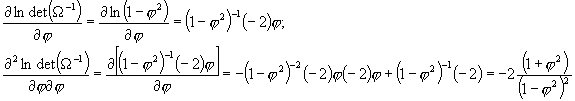
Teraz ; stosując rozumowanie podobne jak powyżej widzimy, że druga pochodna po j z elementów W^-1 jest niezerowa (i wynosi 2) tylko dla (T-2) elementów na głównej przekątnej W^-1. Podstawiając odpowiednie elementy W uzyskujemy:

Ostatecznie

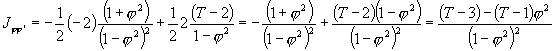
zgodnie z danym powyżej wzorem.

Powyższe wyprowadzenia są po to, żeby Państwo widzieli dlaczego cały wykład Profesor męczył Państwa takimi abstrakcjami – to się w końcu przydaje i pozwala wyprowadzić potrzebne w konkretnych zastosowaniach wzory. W naszym przykładzie dzięki temu będziemy mogli policzyć przybliżony błąd średni szacunku j , i mieć pewne pojęcie o możliwej w naszym modelu sile autokorelacji.

2. UMNRL – model liniowy ze złożoną strukturą stochastyczną

Model liniowy ze złożoną strukturą stochastyczną – znany już z założeń UMNRL – ma postać:

Wektor e ma T-wymiarowy rozkład normalny o wartości oczekiwanej będącej wektorem zerowym oraz macierzy kowariancji V(e) = s²W:

.

Wobec tego (na użytek estymacji MNW) rozkład obserwacji można zapisać następująco:

Funkcję wiarygodności wyprowadza się tak samo, jak w przypadku ogólnym w punkcie 1. , tyle że wartość oczekiwana y nie wynosi g(X;b) tylko Xb. Otrzymujemy więc logarytm funkcji wiarygodności:

który (analogicznie jak w punkcie 1.) koncentrujemy po s² :

.

Jednak ze względu na liniową postać modelu możemy tu uzyskać więcej niż w przypadku modelu nieliniowego: daną wyżej funkcję wiarygodności da się skoncentrować także po b. Aby to uczynić, musimy znaleźć analityczną funkcję maksimum warunkowego l*(b,j ; y) względem b. Zauważmy, że parametry b występują wyłacznie w formie kwadratowej pod logarytmem. Ta forma to uogólniona suma kwadratów reszt znana z własności estymatora Aitkena (zajęcia 17). Wykazano tam, że uogólnioną sumę kwadratów reszt minimalizuje estymator Aitkena [podobne rozumowanie wykorzystujące własności formy kwadratowej przedstawiono przy okazji estymacji MNW modelu SURE]. W funkcji l*(b,j ; y) uogólniona suma kwadratów reszt występuje ze znakiem minus – czyli minimalizacja formy kwadratowej odpowiada maksymalizacji l*(b,j ; y). Szukanym maksimum warunkowym jest więc estymator Aitkena b^_W - jest on funkcją W a więc i funkcją j, jest to maksimum warunkowe względem j:

.

Podstawiamy tą funkcję do l*(b,j ; y) w miejsce b uzyskując:

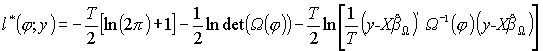
Estymacja

Estymacja MNW modelu liniowego o złożonej strukturze stochastycznej wymaga maksymalizacji NUMERYCZNEJ wyłącznie po elementach wektora j:

Oceny MNW b oraz s² uzyskujemy analitycznie:

W porównaniu z poprzednim przypadkiem upraszcza się także estymator macierzy kowariancji :

(ponieważ w modelu liniowym A(b) = X)

Macierz kowariancji estymatora parametrów struktury stochastycznej j, s² pozostaje taka sama jak w poprzednim przypadku.

Widzimy więc, że przejście na liniową postać zależności strukturalnej pozwala skoncentrować funkcję wiarygodności także po elementach wektora b.

Możemy się zastanawiać, czy skoro wykorzystujemy estymator Aitkena, to czy oceny MNW (b^_NW) są tożsame z ocenami estymatora Aitkena (b^_W)? Odpowiedź brzmi: to zależy jaką ocenę j wykorzystamy do estymatora Aitkena. Jeżeli będzie to ocena MNW, to oczywiście b^_W = b^_NW. Jednak jeżeli użyjemy po prostu innego (zgodnego) estymatora j (np. wykorzystującego statystykę testu D-W – patrz zajęcia 17), to oceny NW i estymatora Aitkena będą się różnić co do wartości.

Poniżej rozważymy dwa przypadki odpowiadające prostej strukturze stochastycznej. Uzyskane wyniki okażą się dostarczać nowego rozumienia znanych już rezultatów.

3. MNRN – model nieliniowy z prostą strukturą stochastyczną

Model nieliniowy o prostej strukturze stochastycznej stanowi szczególny przypadek modelu 1 w którym zakładamy W(j) = I. Wtedy oczywiście nieznane parametry modelu to tylko b, s². Mechanizm powstawania obserwacji zapisujemy jako:

Rozkład składników losowych to T-wymiarowy rozkład normalny o zerowej wartości oczekiwanej i macierzy kowariancji s²I:

_.

Rozkład obserwacji (y) to T-wymiarowy rozkład normalny o wartości oczekiwanej g(X;b) i macierzy kowariancji s²I:

;

(założenia powyższe znamy z Modelu Normalnej Regresji Nieliniowej z Zajęć 9)

Wobec tego funkcja wiarygodności po zlogarytmowaniu ma postać:

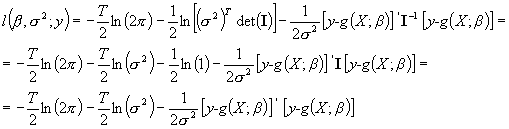
Możemy ją skoncentrować po s² wykorzystując znane już ekstremum warunkowe z punktu 1., tylko w miejsce W podstawimy macierz jednostkową I:

.

Po koncentracji uzyskujemy:

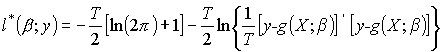
Estymacja

W modelu nieliniowym o prostej strukturze stochastycznej estymacja MNW wymaga NUMERYCZNEJ maksymalizacji skoncentrowanej funkcji wiarygodności l*(b; y) po b. Zauważmy jednak, że wartości b maksymalizujące l*(b; y) minimalizują formę kwadratową [występuje ona w funkcji wiarygodności ze znakiem - ]. Oznacza to, że estymator MNW minimalizuje nieliniową sumę kwadratów reszt, więc jest równoważny z estymatorem nieliniowej MNK b^ znanym z zajęć 9:

_.

Otrzymujemy tu więc uzasadnienie wprowadzonego wcześniej estymatora nieliniowej MNK, który wcześniej realizowaliśmy numerycznie algorytmem Gaussa-Newtona: jest to estymator metody największej wiarygodności. Stąd wzięła się konieczność założenia w MNRN normalności składników losowych; stąd też wynika fakt, że estymator nieliniowej MNK ma własności asymptotyczne (jako estymator MNW).

Ocenę s² uzyskujemy analitycznie:

.

Zauważmy, że w porównaniu ze wzorem na s² w MNRN jedyna różnica polega na tym, że sumę kwadratów reszt dzielimy w MNW przez T a w MNRN przez T-k. W świetle własności asymptotycznych (dla T®¥) odejmowanie lub nie stałej k nie ma (w granicy) znaczenia. W MNRN odejmowanie k możemy interpretować jako pewną poprawkę mającą uwzględnić własności w małej próbie (dla skończonego (niewielkiego) T).

Ostatecznie więc widzimy, że w przypadku modelu nieliniowego o prostej strukturze stochastycznej musimy numerycznie znaleźć oceny parametrów b; MNW sprowadza się tu do nieliniowej MNK – te metody są tożsame – czyli także dają ten sam wynik numeryczny w małej próbie. Widzimy tu więc skąd się biorą założenia MNRN i dlaczego stosuje się tam estymator nieliniowej MNK.

Podstawiając W(j) = I do wzoru na macierz kowariancji estymatora b z punktu 1. otrzymujemy wzór znany z MNRN:

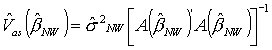
Różnice między MNW a MNRN mogą tu wynikać tylko z dzielenia przez T lub T-k w wykorzystamym wzorze na ocenę s².

W ostatnim, najprostszym przypadku modelu liniowego o prostej strukturze stochastycznej również uzyskamy reinterpretację znanych rezultatów.

4. KMNRL – model liniowy z prostą strukturą stochastyczną

Model liniowy o prostej strukturze stochastycznej stanowi szczególny przypadek modeli 1, 2 oraz 3 – zakładamy tu bowiem zarówno W(j) = I (jak w modelu 3.) oraz y = Xb + e (jak w modelu 2). Nieznane parametry modelu to wciąż b, s². Mechanizm powstawania obserwacji zapisujemy jako:

Rozkład składników losowych to T-wymiarowy rozkład normalny o zerowej wartości oczekiwanej i macierzy kowariancji s²I:

_.

Rozkład obserwacji (y) to T-wymiarowy rozkład normalny o wartości oczekiwanej Xb i macierzy kowariancji s²I:

;

(założenia powyższe znane są nam z Klasycznego Modelu Normalnej Regresji Liniowej z Zajęć 4)

Analogicznie jak w punkcie 3 (tylko wartość oczekiwana y nie wynosi g(X;b) tylko Xb) wyprowadzamy postać logarytmu funkcji wiarygodności otrzymując:

Następnie możemy (tak samo jak poprzednio) skoncentrować l*(b, s²; y) po s²; wykorzystywane maksimum warunkowe zawiera tym razem liniową sumę kwadratów reszt:

uzyskując:

Taką skoncentrowaną funkcję wiarygodności można jednak ANALITYCZNIE zmaksymalizować po b, ponieważ występuje tam minimum (liniowej) sumy kwadratów reszt ze znakiem minus. Estymator zwykłej MNK b^ minimalizuje sumę kwadratów reszt a więc i maksymalizuje funkcję wiarygodności:

Ocenę s² uzyskujemy analitycznie:

.

Widzimy, że w modelu liniowym o prostej strukturze stochastycznej funkcję wiarygodności możemy zmaksymalizować korzystając wyłącznie z technik analitycznych – oceny parametrów uzyskujemy bez wykorzystywania numerycznej maksymalizacji.

Otrzymujemy też reinterpretację wyników znanych z KMNRL – estymator zwykłej MNK b^ okazuje się estymatorem MNW. W ten sposób w KMNRL estymator zwykłej MNK „dziedziczy” ogólne własności estymatorów MNW. Jednakże założenia KMNRL są znacznie mocniejsze od ogólnych założeń MNW, co sprawia, że w KMNRL otrzymujemy znacznie silniejsze własności – w KMNRL znane są własności dokładnie estymatora MNK (a nie tylko asymptotyczne jak w MNW).

Wzór na ocenę asymptotycznej macierzy kowariancji estymatora NW par. b z poprzednich punktów upraszcza się tu do:

co (asymptotycznie, czyli dla T®¥) jest równoważne ze znanym z KMNRL wzorem:

(różnica między nimi wynika z różnicy między s² a - analogicznej jak w punkcie 3.; jednak dla dużego T są one równoważne).

W praktyce kiedy zachodzą założenia KMNRL stosujemy więc wszystkie znane już (zajęcia 4,5,6) techniki – przy założeniach mocniejszych od założeń MNW dysponujemy mocniejszą tezą. Jednak uzyskujemy dodatkowo wiedzę, że estymator zwykłej MNK w KMNRL jest tożsamy z estymatorem MNW.

5. Podsumowanie

W niniejszych zajęciach omawialiśmy estymację MNW jednorównaniowych modeli z egzogenicznymi zmiennymi objaśniającymi (X możemy traktować jak nielosowy) z normalnymi składnikami losowymi. Rozważana była liniowa i nieliniowa postać zależności między X a b oraz prosta / złożona struktura stochastyczna (V(e) = s²I / V(e) = s²W).

Przeprowadzona w powyższych punktach analiza szczególnych przypadków ma na celu lepsze zapoznanie Państwa z estymacją MNW, wyprowadzaniem funkcji wiarygodności i stosowanymi przy tym przekształceniami. Ostatecznie podsumowując cztery przypadki widzimy, że:

· -analityczna maksymalizacja warunkowa (czyli koncentracja l) po s² jest możliwa w każdym z rozważanych przypadków.

· -wprowadzenie złożonej struktury stochastycznej W = W(j) powoduje konieczność numerycznej maksymalizacji funkcji wiarygodności po elementach wektora j

· -rozważanie liniowej postaci zależności zmiennych objaśniających od parametrów y = Xb + e pozwala analitycznie maksymalizować funkcję wiarygodności (czyli ją koncentrować) po b; nieliniowa postać zależności y = g(X;b) + e wymusza numeryczną maksymalizację po b.

Warto także porównać, jaką postać w rozważanych przypadkach ma .

6. Zastosowanie

Ponieważ przypadki III oraz IV dotyczą reinterpretacji stosowanych wcześniej technik, do przećwiczenia pozostają nam przypadki I oraz II, czyli estymacja MNW jednorównaniowych modeli (liniowych i nieliniowych) ze złożoną strukturą stochastyczną.

Jako przykład zależności strukturalnej rozpatrywać będziemy funkcję produkcji translog (model liniowy) oraz CES (model nieliniowy). Jako przykład złożonej struktury stochastycznej przyjmiemy W(j) odpowiadające procesowi AR(1) dla składników losowych (patrz zajęcia 17). Dla CES i Translog mamy oczywiście dwa osobne arkusze.

Aby zrealizować to ćwiczenie, należy rozpatrzyć odpowiednie skoncentrowane funkcje wiarygodności z punktów 1 oraz 2, czyli: l*(b, j; y) oraz l*(j; y). Należy zakodować postać tych funkcji uwzględniając:

1. Konkretną postać W(j) (wtedy dysponujemy wzorem analitycznym na det[W(j)] patrz p.1.).

2. Postać wektora y (y = lnQ) oraz macierzy X (odpowiadającej funkcji translog) oraz funkcji g(X;b) (odpowiadającej zlogarytmowanej funkcji CES)

3. Restrykcje na parametry modelu (patrz niżej)

Następnie używamy solvera (osobno w przypadku CES i Translog) – ustawiając skoncentrowaną funkcję wiarygodności jako „komórkę celu”, a pomocnicze parametry l (bo na parametry modelowe są restrykcje) jako „komórki zmieniane”.

Ponieważ parametr j musi przyjmować wartość z zakresu (-1, 1), dla skutecznego przeprowadzenia numerycznej maksymalizacji musimy to uwzględnić. Jak zwykle, postaramy się tak reparametryzować model, aby pomocnicze parametry l po których „chodzi” solver mogły być dowolne rzeczywiste, a będące ich funkcją parametry „prawdziwe” (j, d, n, g etc.)– wchodzące do funkcji wiarygodności – miały zawsze „właściwe” wartości. Tutaj ponieważ j musi należeć do przedziału (-1, 1), możemy wykorzystać np. funkcję arcus tangens: za j podstawimy arc tg komórki rzeczywiście zmienianej przez solver . W excelu funkcja arcus tangens to ATAN(.); jednak przyjmuje ona wartości od -p/2 do p/2. Musimy to uwzględnić stosując odpowiednie skalowanie. Ostatecznie: formuła =ATAN(A1)*2/PI() będzie zwracać wartość j wykorzystywaną we wszystkich wzorach, natomiast solver jako „komórkę zmienianą” będzie miał „A1” (A1 to oczywiście tylko przykład), co zapewni stabilność przebiegu algorytmu.

Podobnie, ponieważ d, n, g muszą być dodatnie, w przypadku tych parametrów wykorzystujemy funkcję exp(.). W przypadku parametru r nie musimy uwzględniać restrykcji – mają one charakter ekonomiczny; możemy je narzucić lub nie, ale kiedy nie będą spełnione, to funkcja wiarygodności będzie określona, tymczasem złamanie pozostałych restrykcji skutkuje np. logarytmowaniem liczb ujemnych, co przerywa obliczenia i pozbawia nas jakichkolwiek wyników.

Ostatecznie więc w arkuszu robimy wektor l komórek po których chodzi solver, i obok wektor parametrów modelu, które są funkcjami l i wchodzą do funkcji wiarygodności. Tam np. fi=ATAN(A1)*2/PI(), gamma=exp(A2), delta=exp(A3); ni=exp(A4); rho=A5 (to dla funkcji CES; wektor l jest od A1 do A5)

Po zmaksymalizowaniu skoncentrowanej funkcji wiarygodności oceny pozostałych parametrów otrzymujemy analitycznie. Aby otrzymać błędy średnie szacunku parametrów należy skorzystać ze wzorów podanych w punktach 1, 2 dla b oraz w p. 1. dla s², j.

Zadanie laboratoryjne część A:

Korzystając z powyższych wzorów oszacować MNW statyczną funkcję produkcji translog na danych maddala.xls przyjmując gaussowski [czyli o rozkładzie normalnym] proces AR(1) dla składników losowych. Proszę podać:

1. oceny MNW parametrów b, s², j.
2. przybliżone błędy śr. szacunku b, s², j.
3. przybliżony błąd średni szacunku efektu skali dla T = 1,...,39
4. ustalając j = 0 (tak, żeby solver jej nie zmieniał),, przeprowadzić powtórnie estymację (solverem) i pokazać, że uzyskane wyniki są takie same jak z estymatora zwykłej MNK w KMNRL.

Wyniki dla porównania:

Translog statyczny:

logarytm funkcji wiarygodności po zmaksymalizowaniu: 92.29916

ocena MNW j = 0.924558

przybliżony bł. średni szacunku j^_NW [bez aproksymacji krótszym wzorem]= 0.054174

[ proszę o potwierdzenie wyników bo nie jestem w 100% pewien]

Zadanie laboratoryjne część B:

Korzystając z powyższych wzorów oszacować MNW dynamiczną lub statyczną funkcję CES na danych maddala.xls przyjmując gaussowski [czyli o rozkładzie normalnym] proces AR(1) dla składników losowych. Proszę podać:

5. oceny MNW parametrów r, d, n, g, s², j.
6. przybliżone błędy śr. szacunku r, d, n, g, s², j.
7. przybliżony błąd średni szacunku elastyczności EL_Q/L oraz EL_Q/K dla T = 1,...,39, zrobić odpowiednie wykresy: elastyczność +- dwa przybliżone błędy śr. szacunku.
8. ustalając j = 0 (tak, żeby solver jej nie zmieniał), przeprowadzić powtórnie estymację (solverem) i pokazać, że uzyskane wyniki są takie same jak z estymatora nieliniowej MNK w MNRN.

Wyniki dla porównania:

CES statyczny:

logarytm funkcji wiarygodności po zmaksymalizowaniu: 86.445454

ocena MNW j = 0.772886839

ocena MNW r = -0.16087

przybliżony bł. średni szacunku j^_NW [bez aproksymacji krótszym wzorem]= 0.099231021

ocena MNW El Q/K dla t=2: 0.552259

Przybliżony błąd śr. szacunku oceny El Q/K dla t=2: 0.106777

[ proszę o potwierdzenie wyników bo nie jestem w 100% pewien]

(wyliczanie błędów średnich szacunku elastyczności dla CES jest omówione w zajęciach 22)