Zajęcia 22

Estymator MNW dla różniczkowalnych funkcji oryginalnych parametrów

Często dysponujemy ocenami MNW pewnych strukturalnych parametrów modelu, jednak interesuje nas wnioskowanie o pewnych (nieliniowych często) funkcjach tych parametrów. Przykładowo, szacujemy parametry funkcji produkcji, ale interesuje nas wnioskowanie o elastycznościach – które są funkcjami parametrów technologii. Możemy szacować układ funkcji popytu, ale interesuje nas wnioskowanie o elastycznościach popytu itd.

W związku z tym powstaje pytanie: jak uzyskać oceny NW oraz ocenę macierzy kowariancji estymatora NW dla funkcji oryginalnych parametrów.

Podstawowe własności estymatora MNW

Najpierw przypomnijmy podstawowe własności estymatora MNW oryginalnych parametrów:

Oznaczmy:

q - k-wymiarowy wektor-kolumna oryginalnych parametrów modelu

wtedy:

(estymator MNW uzyskujemy jako maksimum funkcji wiarygodności)

[to nie jest super ścisłe – gdyby ktoś chciał dokładniej zrozumieć teorię asymptotyczną to trzeba byłoby to uściślić. Ale do naszych celów takie ujęcie powinno być OK. – proszę tylko mieć świadomość, że argument „asymptotyczny” wymaga bardziej skomplikowanych wyprowadzeń formalnych]

(estymator MNW ma asymptotyczny rozkład normalny o wartości oczekiwanej równej wartości nieznanych parametrów q i macierzy kowariancji zadanej jako:)

(... odwrotność macierzy informacyjnej)

Oznaczmy teraz interesującą nas funkcję parametrów przez h:

(tu l reprezentuje np. wartość elastyczności, a h(q) reprezentuje elastyczność jako funkcję parametrów)

Zakładamy, że funkcja h jest różniczkowalna względem q.

Oczywiście h może być wektorem i reprezentować więcej, np. q funkcji – ustawiamy je wtedy w wektor – kolumnę:

.

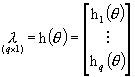Wtedy

1. uzyskujemy następująco:

(zgodnie z tzw. zasadną niezmienniczości NW)

(czyli aby uzyskać ocenę NW np. elastyczności, do wzoru na elastyczność musimy podstawić oceny NW parametrów.. ta własność wygląda bardzo prosto, ale jest nietrywialna i ważna)

wtedy oczywiście ma ogólne własności estymatorów MNW, czyli np.

(to nie jest własność trywialna, bo: oczywiście wstawiając oceny parametrów do wzoru na elastyczność uzyskujemy JAKIŚ estymator, ale tutaj ważny jest fakt, że uzyskany tak estymator TEŻ ma własności MNW – więc tak samo można np. testować hipotezy o elastycznościach lub o innych funkcjach parametrów i budować dla nich przedziały ufności. czyli literek NW nie można zgubić, bo traci się sens – dalej możemy testować dlatego, że przy lambda jest nie tylko daszek ale i NW.

2. otrzymujemy tak:

Rozważmy najpierw macierz A(q) wymiaru (q´k) pochodnych cząstkowych funkcji h względem q:

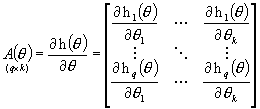
W kolejnych wierszach mamy pochodne kolejnych funkcji [w i-tym wierszu pochodne h_i(q)], natomiast w kolejnych 1,2,...,k kolumnach każdego i-tego wiersza pochodne h_i(q) po q₁, q₂, ...,q_k.

możemy przybliżać jako:

(wyprowadzenie zostało podane na wykładzie).

Zgodny estymator jest zdefiniowany jako:

_.

Wzór dany powyżej wykorzystuje pewne przybliżenie. Więc w praktyce przybliżenia są dwa: jedno wynika z odwoływania się do asymptotyki – nie wiemy, jak dobre lub jak złe w konkretnej próbie jest asymptotyczne przybliżenie; drugie przybliżenie wynika z zastosowania aproksymacji przy użyciu pierwszych pochodnych.

Uwaga 1. Macierzy A(q) pochodnych funkcji h po parametrach q nie należy mylić z macierzą A(b) pochodnych g(X; b) po b (czyli części wektora q) – por. zajęcia 21.

Uwaga 2. Kolejność kolumn w macierzy A(q) musi odpowiadać kolejności wierszy/kolumn w macierzy - czyli być wyznaczona przez kolejność parametrów w q.

Uwaga 3. Jeżeli h(q) jest funkcją tylko niektórych parametrów w q, wystarczy rozpatrywać niezerowe elementy h(q), i oczywiście odpowiadający im blok w .

Przykłady:

Przykład 1. Przypomnijmy sobie wnioskowanie o elastycznościach funkcji Translog. W zajęciach 5 pokazywaliśmy, jak obliczyć błędy średnie szacunku elastyczności w translog korzystając z wnioskowania o liniowej kombinacji parametrów. Obecnie rozpatrujemy bardziej ogólny przypadek nie tylko liniowych, ale i ogólnie różniczkowalnych funkcji parametrów. Wobec tego znany sposób wnioskowania musi być szczególnym przypadkiem znanej metody. Przypomnijmy:

Funkcja translog:

lnQ_t = a₀ + a₁ln K_t + a₂ln L_t + a₃ ln² K_t + a₄ ln² L_t + a₅ lnK_t lnL_t + e_t

El_Q/K^ = a₁ + a₃ 2 ln K_t + a₅ lnL_t

b’ = [ a₀ a₁ a₂ a₃ a₄ a₅ ]

wobec tego:

c’ = [0 1 0 2lnK_t 0 lnL_t]

Zauważmy teraz, że jeśli przyjmiemy El_Q/K = h(q), to c’ = A(q) – wektor c’ to wektor pochodnych El_Q/K po parametrach b. W ten sposób można łatwo skojarzyć nowy wzór dany powyżej ze znanym już Państwu sposobem postępowania.

Przykład 2. Rozważmy estymację MNW funkcji CES z autokorelacją – przykład laboratoryjny z zajęć 21. Elastyczność substytucji w funkcji CES ma postać:

Jeżeli mamy oszacowaną funkcję CES:

i chcemy znać błąd średni szacunku elastyczności substytucji.

Mamy:

,. Ponieważ , wobec tego:

. Natomiast żeby policzyć :

wyliczamy , a następnie otrzymujemy:

W wektorze h(q) występuje wiele zer – a dokładniej tylko jeden niezerowy element, możemy powyższe sprowadzić do:

Przykład 3. Rozważmy w dalszym ciągu estymację NW dwuczynnikowej funkcji CES. Dotychczas nie dysponowaliśmy metodami pozwalającymi wyliczyć błąd średni szacunku elastyczności w funkcji CES.

W tym przypadku .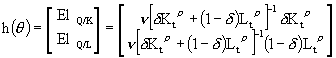

Zauważmy, że elastyczności są funkcją wyłącznie parametrów d, n, r; więc wystarczy rozważyć:

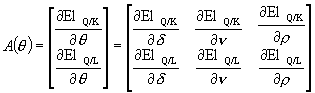
Oczywiście A(q) będzie funkcją konkretnych poziomów nakładów K_t oraz L_t, dla których wyliczamy wartość elastyczności. Dalej wykorzystujemy odpowiedni blok odpowiadający d, n, r:

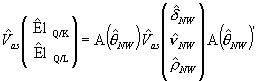
(postać pochodnych sobie Państwo policzą, nie chcę nikomu odbierać przyjemności J)

Jeżeli nie interesują nas kowariancje ocen elastyczności, możemy wyliczyć osobno wiersze A(q) i przemnożyć osobno razy blok z oceny macierzy kowariancji .

Jak sprawdzić, czy nie pomyliliśmy się w pochodnych? Pewnego pośredniego sprawdzianu dostarcza następujące rozumowanie: aby policzyć błąd średni szacunku SUMY elastyczności musielibyśmy rozważyć h(q) = El_Q/K+ El_Q/L . Wtedy A(q) będzie zawierać pochodną sumy, czyli sumę pochodnych które wyliczyliśmy powyżej. Ale suma elastyczności to efekt skali, czyli parametr n w funkcji CES. Ale błąd średni szacunku parametru n możemy dostać bezpośrednio z i powinno wyjść to samo. Czyli A(q) dla sumy pochodnych tj. suma wyliczonych osobno pochodnych musi wybierać z macierzy element odpowiadający parametrowi n; czyli A(q) dla sumy elastyczności musi być wektorem zerowym z jedną jedynką na tym miejscu które odpowiada parametrowi n - jeśli obliczone dla elastyczności pochodne w A(q) nie sumują się do takiego wektora, to coś jest źle. Można to sprawdzić nawet tylko numerycznie w Excelu.

Po co to wszystko? dla wnioskowania..

Tutaj pokazujemy jak wyliczyć . Ale co nam to daje??

po pierwsze możemy przeprowadzać testy. Hipotezy dotyczące rozważanej funkcji parametrów mogą być testowane przy pomocy testu typu t – studenta (jak w KMNRL). Możemy to zrobić, bo z macierzy możemy wyliczyć przybliżony błąd średni szacunku rozważanej funkcji parametrów.

Testując parę hipotez:

H₀: l = l* H₁: l ¹ l*

[oczywiście w praktyce zamiast l* jest jakaś liczba i trzeba napisać, co to jest l - podać np. l = 1/(b₁ + b₂) ]

Konstruujemy więc statystykę typu t o postaci:

i standardowo testujemy. Różnice w porównaniu z KMNRL są dwie:

po pierwsze test ma charakter asymptotyczy, czyli w praktyce przybliżony (bo odwołujemy się do asymptotycznego rozkładu statystyki testowej)

po drugie wartości krytyczne powinniśmy wyliczać z rozkładu normalnego standaryzowanego (dla poziomu istotności równego 0.05 warto znać wartości krytyczne na pamięć). Nie mamy żadnych podstaw teoretycznych do stosowania rozkładu t-Studenta. Możemy stosować rozkład t jako „poprawkę na małą próbę” – jednak dla takiego postępowania nie mamy uzasadnienia w teorii, to po prostu pewna praktyka. Dla liczby obserwacji większej od 50 różnica między rozkładem t a normalnym jest już zaniedbywalna, więc przy większym T nie ma różnicy.

Podobnie możemy zbudować przedział ufności dla badanej funkcji parametrów – postępujemy analogicznie jak w KMNRL pamiętając jednak, że wyniki są przybliżone a stosować powinniśmy w zasadzie rozkład normalny.

Przykład (ciąg dalszy przykładu 2 powyżej)

przypuśćmy, że uzyskaliśmy realizację wynoszącą 0,85. Ponadto załóżmy, że ocena MNW r to= 0.5. W związku z tym ocena MNW elastyczności substytucji to 1/(1-0.5) = 2.

Jeżeli chcemy zweryfikować hipotezę zerową mówiącą, że elastyczność substytucji jest równa 1, zgodnie z tym co powyżej, wyliczamy realizację statystyki jako: (2 – 1)/Ö0.85 = 1.085. Dwustronna 5% wartość krytyczna z rozkładu normalnego to 1.96 – wobec tego na poziomie istotności 0.05 nie ma podstaw do odrzucenia hipotezy mówiącej że elastyczność substytucji jest tu równa 1. Pamiętamy jednak, że jest to test asymptotyczny, przybliżony.

Analogicznie jak w KMNRL możemy dokonać estymacji przedziałowej elastyczności substytucji. Stosując standardowe wzory uzyskujemy:

(2-1.96*Ö0.85, 2+1.96*Ö0.85) = (0.193 , 3.81)

interpretacja jest standardowa (jak w KMNRL – zajęcia 4), tylko pamiętamy, że jest to pewne przybliżenie, co można zaznaczyć:

to pojedyncza realizacja najkrótszego przedziału o końcach losowych pokrywającego nieznaną wartość parametru z prawdopodobieństwem wynoszącym OKOŁO 0.95