Zajęcia 23

Łączna (systemowa) estymacja modeli wielorównaniowych: 3MNK oraz MNW dla nieliniowego układu SURE

0. Wstęp

Z łączną estymacją modeli wielorównaniowych zetknęliśmy się już w przypadku systemów SURE. Staraliśmy się tam zapisać model wielorównaniowy jako jednorównaniowy (wykorzystując strukturę „kroneckerowską”), a następnie zastosować znane metody estymacji modeli jednorównaniowych. W ten sposób stosujemy estymator Aitkena do systemu SURE (procedura Zellnera – zaj. 19) oraz estymację MNW liniowego modelu jednorównaniowego ze złożoną strukturą stochastyczną do SURE (estymacja MNW SURE – zaj. 20). Dotąd szacowaliśmy w ten sposób modele liniowe o prostej strukturze (jak SURE). Teraz zajmiemy się metodami pozwalającymi na łączne szacowanie całego układu równań (systemu) dla modeli nieliniowych. Jako szczególny przypadek rozpatrzymy liniowe modele o równaniach łącznie współzależnych.

Jednak zanim przejdziemy do szczegółowego omawiania metod łącznej estymacji modeli wielorównaniowych, spróbujmy poświęcić trochę uwagi ich ogólnym własnościom. Chodzi o to, dlaczego stosujemy „łączną” estymację, jaka to jest „niełączna” estymacja i czym się one różnią. Ponieważ łączna estymacja jest bardziej skomplikowana, chcemy wiedzieć jaką odnosimy korzyść przechodząc z metod „równanie po równaniu” na metody systemowe (estymacji łącznej). W niektórych przypadkach nie możemy korzystać z metod „równanie po równaniu” – wtedy musimy odwołać się do estymacji łącznej – pokażemy, kiedy tak jest.

Rozważmy przykład estymacji systemu SURE. Możemy taki system szacować zwykłą MNK równanie po równaniu. Oczywiście nie jest to łączna estymacja, bo każde równanie szacujemy osobno. Estymator zwykłej MNK jest zgodny. Jednak do systemu SURE stosowaliśmy procedurę Zellnera (czyli estymator Aitkena dla całego systemu zapisanego jako model jednorównaniowy). Robimy to, aby uzyskać większą efektywność – „bardziej dokładne” oszacowania parametrów. Różnica jest tu taka, jak między zwykłą MNK a estymatorem UMNK/EUMNK w UMRL (por. zaj. 17). Procedura Zellnera poprawia efektywność oszacowań parametrów (w porównaniu ze zwykłą MNK), ponieważ bierzemy pod uwagę kowariancje między równoczesnymi składnikami losowymi różnych równań. Wykorzystujemy więc informację o systemie jako całości – o zależnościach POMIĘDZY równaniami. Te zależności przy szacowaniu każdego równania osobno (metodami „niesystemowymi”, „niełącznymi”) są ignorowane.

Widzimy więc, że metody systemowe mają przewagę nad metodami „równanie po równaniu” polegającą na większej efektywności wynikającej z uwzględnienia pełniejszej informacji. Ponadto metody „równanie po równaniu” można stosować tylko wtedy, kiedy zależności pomiędzy równaniami da się pominąć bez naruszenia najistotniejszych problemów.

Teoretyczna przewaga metod systemowych nad metodami „równanie po równaniu” jest podobna, jak przewaga UMNK nad MNK w UMRL – tam jednak w praktyce stosujemy nie UMNK lecz EUMNK, więc szacujemy macierz W. Ponieważ możemy źle przyjąć strukturę W lub „źle trafić” w małej próbie z estymatorem j, przewaga EUMNK nad MNK nie jest już tak oczywista. Podobnie jest w tym przypadku – przechodząc z warunków idealnych na praktyczne przewaga metod systemowych nad metodami „równanie po równaniu” nie jest tak oczywista. Powody w tym przypadku mogą być dwa:

1. W małej próbie oszacowanie macierzy równoczesnych kowariancji może być „źle trafione” – źle oddaje prawdziwą macierz równoczesnych kowariancji, przez co wnosi nieprawdziwą informację i może nawet pogorszyć efektywność w stosunku do metod „równanie po równaniu”.
2. Błąd specyfikacji w jednym równaniu „roznosi się” po całym systemie. W przypadku metod „równanie po równaniu” błąd specyfikacji jednego równania ma ograniczony wpływ na oszacowania parametrów innych równań.

Są jednak przypadki, gdy MUSIMY stosować metody systemowe. Przedstawione wyżej heurystyczne rozumowanie sugeruje, że jest tak w przypadku gdy zależności między równaniami są „niezaniedbywalne” w ramach rozpatrywanego problemu. Może to mieć miejsce wtedy, gdy zachodzą związki między PARAMETRAMI różnych równań. Może np. interesować nas:

A) Wnioskowanie o funkcjach parametrów różnych równań Przykładowo chcemy wnioskować o wielkości będącej funkcją parametrów różnych równań – wtedy aby otrzymać np. błąd średni szacunku tej wielkości, musimy uwzględnić kowariancje estymatora oryginalnych parametrów, co wymaga łącznej estymacji.

B) Narzucenie restrykcji wiążących parametry różnych równań. Jeżeli chcemy narzucić (a priori lub w celu testowania) restrykcję mówiącą np. że jeden parametr w pewnym równaniu jest równy innemu parametrowi w innym równaniu, to musimy te dwa równania szacować równocześnie, czyli właśnie łącznie.

Związki pomiędzy parametrami różnych równań mogą mieć charakter restrykcji równościowych (liniowych bądź nieliniowych). Poznamy metody pozwalające uwzględniać takie (równościowe) restrykcje (wymagające np. by suma pewnych parametrów z różnych równań wynosiła 1). Można rozważać także restrykcje nierównościowe, jednak tu sprawa jest trudniejsza i nie będziemy się nimi zajmowali. Problem komplikuje się ponadto w przypadku, gdy restrykcje są zależne od danych. Podsumowując, metody systemowe pozwalają nam uwzględnić:

Ø równoczesne kowariancje składników losowych różnych równań

Ø zależności pomiędzy parametrami różnych równań na użytek estymacji i wnioskowania

W tych zajęciach:

W niniejszych zajęciach zajmiemy się omówieniem następujących systemowych metod estymacji

· trójstopniowej MNK (3MNK) dla estymacji liniowych modeli wielorównaniowych o równaniach współzależnych,

· metodą największej wiarygodności dla nieliniowych systemów typu SURE.

Ponieważ postać zredukowana z restrykcjami (RRF) modelu liniowego o równaniach łącznie współzależnych jest szczególnym przypadkiem nieliniowego modelu SURE (bo jest nieliniowa ze względu na oryginalne parametry postaci strukturalnej) – będziemy dysponować dwiema metodami systemowymi estymacji liniowych modeli wielorównaniowych o równaniach współzależnych: 3MNK oraz MNW.

Oczywiście MNW dla nieliniowego systemu SURE ma szersze zastosowanie – przykład wykorzystujący estymację systemów wydatków będzie przedmiotem kolejnych zajęć.

Uwagi terminologiczne: Trójstopniowa MNK to po ang. Three-stage Least Squares, (3SLS); MNW dla całego systemu to “MNW z pełną informacją” (Full-Information Maximum Likelihood, FIML), natomiast MNW oddzielnie dla pojedynczego równania to MNW z niepełną informacją (Limited-Information Maximum Likelihood, LIML) – tą metodą nie będziemy się zajmować.

1. Trójstopniwa MNK (3MNK) – metoda łącznej estymacji

liniowych modeli wielorównaniowych o równaniach łącznie współzależnych

Trójstopniowa MNK jest rozwinięciem dwustopniowej MNK w sposób pozwalający uwzględnić równoczesne kowariancje składników losowych postaci strukturalnej. Powtórzmy, chodzi o uwzględnienie kowariancji między składnikami losowymi różnych równań postaci strukturalnej (dla tego samego numeru obserwacji). Kowariancje pomiędzy składnikami losowymi dla różnych numerów obserwacji są tu zerowe (wykluczamy autokorelację). Podobnie zakładamy stałość wariancji składnika losowego jednego równania dla wszystkich obserwacji. Założenia o strukturze stochastycznej są więc tu analogiczne jak w systemie SURE. Zapiszmy więc przykładowy n-równaniowy model liniowy o równaniach współzależnych:

; , ,

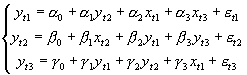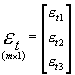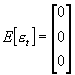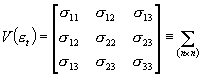
( t = 1,...,T )

UWAGA: notacja i problematyka w tych zajęciach jest kontynuacją notacji i problematyki zajęć 14, proszę więc upewnić się że znają Państwo zajęcia 14

S, czyli macierz równoczesnych kowariancji składników losowych e_t, to macierz stopnia n symetryczna (a więc i kwadratowa), dodatnio określona [S jako macierz kowariancji musi być nieujemnie określona, ale będziemy ją odwracać – wymagamy jej nieosobliwości – czyli łącznie dodatniej określoności S; przypadek osobliwej macierzy S będzie specjalnie rozważany]. Ponadto S nie zależy od t – jest taka sama dla każdego numeru obserwacji.

Takiej postaci strukturalnej nie możemy wprost szacować ani zwykłą MNK równanie po równaniu ani korzystając z procedury Zellnera, ponieważ zmienne łącznie współzależne y_ti będące zmiennymi objaśniającymi (w równaniach po prawej stronie) – są „silnie zależne” [funkcyjnie] od składników losowych tego samego równania, więc estymator MNK lub Zellnera nieznanych parametrów będzie NIEZGODNY. Podobnie nie można by było wprost zastosować tu znanej Państwu postaci estymatora MNW dla SURE (nawet przy założeniu normalności e_t) – ponieważ rozważając rozkład obserwacji trzeba byłoby uwzględnić losowość y_ti występujących po prawej stronie i ich związek z e_t.

W celu uzyskania zgodnych oszacowań parametrów postaci strukturalnej stosowaliśmy 2MNK. Polegała ona na tym, że:

I) w pierwszym kroku szacowaliśmy zwykłą MNK postać zredukowaną bez restrykcji (URF), czyli Y = XP+V. Ponieważ w każdym równaniu występują tu te same zmienne objaśniające (X), procedura Zellnera dla estymacji P (bez uwzględnienia restrykcji wynikających z P=-GB^-1) sprowadza się do zwykłej MNK równanie po równaniu. Następnie uzyskiwaliśmy teoretyczne wartości zmiennych łącznie współzależnych Y^ = XP^.

II) w drugim kroku wykorzystujemy uzyskane wartości teoretyczne zmiennych łącznie współzależnych Y^, wstawiając je po PRAWEJ stronie do postaci zredukowanej w miejsce y_ti. Ponieważ y_ti^ są „słabo zależne” od e_t, tak zmodyfikowaną postać strukturalną możemy szacować MNK równanie po równaniu uzyskując ZGODNE oceny parametrów.

Dla celów estymacji przyjmowaliśmy następującą notację:

d⁽ⁱ⁾ – nieznane parametry i-tego równania (czyli m_i nieznanych elementów w i-tej kolumnie B oraz k_i nieznanych elementów w i-tej kolumnie G)

– macierz zmodyfikowanych zmiennych objaśniających i-tego równania postaci strukturalnej, gdzie wartości y_ti zastąpiono przez odpowiednie wartości teoretyczne y_ti^,

Oceny 2MNK nieznanych parametrów i-tego równania to:

W tej procedurze nie uwzględniamy jednak równoczesnych kowariancji e_t. Pamiętamy, że w przypadku modelu SURE przechodząc od estymacji MNK równanie po równaniu do procedury Zellnera (czyli uwzględniając równoczesne kowariancje składników losowych) uzyskujemy teoretycznie poprawę efektywności oszacowań. W przypadku trójstopniowej MNK generalizujemy 2MNK w analogiczny sposób i w tym samym celu. Po wstawieniu do postaci strukturalnej wartości teoretycznych zmiennych łącznie współzależnych po PRAWEJ stronie, zmodyfikowany układ równań traktujemy jak model SURE i szacujemy stosując procedurę Zellnera. W ten sposób w 3MNK łączymy dwa aspekty:

• stosujemy zmienne Z_i^ w miejsce Z_i by zapewnić zgodność estymatora (co można ściśle interpretować na gruncie teorii zmiennych instrumentalnych (instrumental variables, IV)
• szacujemy postać strukturalną łącznie jako SURE by uwzględnić równoczesne kowariancje składników losowych i poprawić w ten sposób efektywność estymatora

[Estymator 3MNK łączy więc cechy estymatora IV oraz estymatora Aitkena/procedury Zellnera ]

Uwzględniając notację z Zajęć 14 i przystosowując ją do układu SURE, postać strukturalną liniowego modelu wielorównaniowego możemy łącznie zapisać jako:

gdzie:

;;;

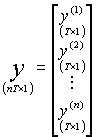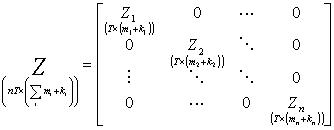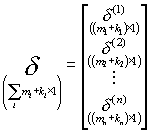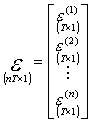
Wtedy macierz kowariancji składników losowych e ma postać:

Odpowiednik estymatora Aitkena w takim systemie (biorący pod uwagę macierz równoczesnych kowariancji) to:

,

taki estymator byłby niezgodny ze względu na obecność Y_i w Z. Jeżeli jednak uwzględnimy dodatkowo przejście z Z_i na Z_i^, (czyli zastosujemy zmienne instrumentalne Y_i^ w miejsce Y_i) oznaczając:

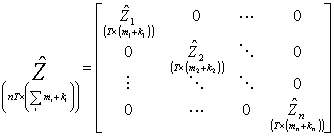
(por. oznaczenia w zajęciach 14),

uzyskamy estymator 3MNK o postaci:

Zauważmy jednak, że ciągle posługujemy się tu znaną macierzą S (jak w UMNK), podczas gdy w praktyce musimy ją szacować. Ostatecznie szacowany estymator 3MNK, wykorzystywany w praktyce (analogicznie jak estymator EUMNK) ma postać:

,

gdzie macierz S (ocenę S) uzyskujemy analogicznie jak w procedurze Zellnera:

,

Pamiętamy jednak, że w celu estymacji macierzy równoczesnych kowariancji w SURE wykorzystywaliśmy reszty ZGODNEGO estymatora (w SURE estymator MNK jest zgodny). Tutaj podobnie musimy użyć reszt zgodnego estymatora, jednak estymator zwykłej MNK zgodny już nie jest. W związku z tym wykorzystane powyżej to reszty (zgodnej) 2MNK (dla i-tego równania) – te same które w 2MNK wykorzystywane są do wyliczenia s²_i .

Ocenę asymptotycznej macierzy kowariancji estymatora 3MNK uzyskujemy (analogicznie jak w procedurze Zellnera) jako:

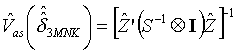
W przypadku 3MNK (w przeciwieństwie do procedury Zellnera) iterowane wyliczanie kolejnych reszt, ocen S, ocen parametrów itd. nie prowadzi do uzyskania ocen MNW – w ogóle nie poprawia w żaden sposób własności estymatora. Intuicyjnie można się tego spodziewać, ponieważ cały czas wykorzystujemy te same Y_i^ wyliczone z URF.

Własności estymatora 3MNK (tylko nieformalnie zarysowane):

1) zgodność

2) jest asymptotycznie najefektywniejszy w pewnej klasie estymatorów (do której należy 2MNK, więc jest bardziej efektywny od 2MNK) [w pewnej klasie estymatorów zmiennych instrumentalnych]

3) jeżeli założymy normalność e, jest asymptotycznie równoważny estymatorowi MNW z pełną informacją (opisanemu poniżej) (3MNK ma ten sam rozkład asymptotyczny) – ale to nie oznacza numerycznej równoważności oszacowań w skończonej próbie.

Szczególne przypadki 3MNK:

1) w sytuacji gdy wiemy a priori, że S jest macierzą diagonalną, czyli równoczesne kowariancje składników losowych są zerowe, metoda systemowa wykorzystująca „efekt SURE” oczywiście nie poprawia efektywności. W takim przypadku (analogicznie jak w SURE) 3MNK sprowadza się do 2MNK. Taki sąd a priori jest jednak dość mocny i w praktyce zakładamy raczej niezerowe równoczesne kowariancje.

2) Kiedy wszystkie równania są jednoznacznie identyfikowalne, 3MNK sprowadza się do 2MNK.

Przypadek osobliwej macierzy równoczesnych kowariancji:

W niektórych przypadkach mamy do czynienia z osobliwą macierzą równoczesnych kowariancji S.

1. Może to mieć miejsce, gdy (jak w modelu Kleina) niektóre równania mają charakter tożsamości i są pozbawione składników losowych. Wtedy wymagamy dodatniej określoności tego bloku S, który odpowiada kowariancjom między równaniami rzeczywiście posiadającymi składniki losowe. Ponieważ równania będące tożsamościami (a więc spełnione dokładnie) nie posiadają zwykle nieznanych parametrów, w praktyce w takim przypadku w ostatnim kroku 3MNK rozważamy odpowiedni blok S i tylko te równania, które mają nieznane parametry.

Przykładowo, w modelu Kleina macierz rozważamy tylko 1,2 i 3 równanie, do wzorów podstawiamy Z^ zbudowane z Z₁^, Z₂^ i Z₃^ oraz odpowiednio blok stopnia 3 macierzy S oraz jego oszacowanie uzyskane z reszt MNK pierwszych 3 równań.

2. W niektórych przypadkach wszystkie równania zawierają nieznane parametry oraz składniki losowe, lecz a priori zakładamy zależność pomiędzy składnikami losowymi która implikuje osobliwość S. Tak jest w przypadku systemów wydatków szacowanych w postaci równań udziału z addytywnymi składnikami losowymi. Udziały obserwowane sumują się do jedności (na mocy konstrukcji danych), udziały teoretyczne sumują się do jedności dzięki odpowiednim restrykcjom nałożonym na parametry, więc składniki losowe muszą się sumować do zera, aby zachodziły wszystkie równości. Oznacza to, tylko (n-1) równoczesnych składników losowych jest swobodnych, wobec czego S jest rzędu (n-1). W takim przypadku musimy tak przeformułować model, aby doprowadzić go do postaci z nieosobliwą macierzą równoczesnych kowariancji (zwykle mamy wtedy n-1 równań), ale musimy to zrobić tak, aby w zmodyfikowanym układzie identyfikowalne były wszystkie interesujące nas parametry.

Zauważmy, że powyżej w przypadku 2 wykraczamy nieco poza zakres stosowalności 3MNK tak jak to powyżej opisano. Systemy wydatków są zwykle nieliniowymi modelami typu SURE, lecz ponadto, co ważniejsze, omawiając 3MNK zakładaliśmy brak powiązań pomiędzy parametrami różnych równań.

3MNK tak jak opisana powyżej, pozwala na wnioskowanie o funkcjach parametrów różnych równań (patrz przykłady na końcu), nie pozwala jednak na narzucanie restrykcji na parametry (by uwzględnić je w estymacji lub testować).

W przypadku 3MNK można zastosować metody pozwalające np. narzucić liniowe restrykcje na parametry (analogicznie jak w przypadku zwykłej MNK o czym nie mówiliśmyJ) – zainteresowanych odsyłam do Zasad Ekonometrii Henri Theila (str. 516 i n.). Narzucanie restrykcji wiążących parametry różnych równań przedstawione zostanie poniżej w kontekście MNW z pełną informacją.

2. Metoda największej wiarygodności z pełną informacją (FIML) dla estymacji nieliniowych systemów typu SURE

( tymczasowo w skrócie J)

W tym punkcie rozpatrzymy MNW dla nieliniowych systemów SURE. Zakładamy, że X są egzogeniczne (można je traktować jak nielosowe) (jak powyżej) oraz, że składniki losowe mają rozkład normalny. Ściśle, w rozpatrywanej tu wersji, zakładamy więc, że X nie zawierają opóźnionych Y; ale daje się to uchylić.

Nieliniowy model SURE zapisujemy inaczej niż liniowy: blokowo – diagonalna struktura „kroneckerowska” jest potrzebna żeby mnożenie odpowiednich macierzy się zgadzało, a więc dotyczy tylko modelu liniowego. W nieliniowym modelu SURE wprowadzamy zapis zbliżony do postaci zredukowanej modelu wielorównaniowego:

Y = G(X;b) + E

(powyższe macierze są wymiaru (T ´ n), kolumny odpowiadają kolejnym równaniom, wiersze kolejnym obserwacjom)

Funkcja wiarygodności [zlogarytmowana] (wyprowadzenie analogiczne jak w zajęciach 20 J) ma postać:

Taką funkcję możemy skoncentrować po S, w tym celu wykorzystujemy funkcję warunkowego maksimum l(b,S; y) przy ustalonym b - o postaci znanej z zajęć 20.

Tu nastąpił konflikt oznaczeń którego stałem się niewinną ofiarą. Nabożeństwo żałobne nie odbędzie się, prosimy o nieskładanie kondolencji, autor zostanie pochowany w tajemnicy pomiędzy samobójcami i rozwodnikami.

ZADANIE:

Oszacować 3MNK model Kleina; otrzymać oceny parametrów i ich przybliżone błędy średnie szacunku.

Wyniki dla sprawdzenia (kolejność może być dziwna, ale pierwsze 4 są dla pierwszego równania itd..)

Oceny 3MNK	as bł śr
0.12489	0.108129
0.790081	0.037938
0.163144	0.100438
16.44079	1.304549
-0.01308	0.161896
0.755724	0.152933
-0.19485	0.032531
28.17785	6.79377
0.400492	0.031813
0.181291	0.034159
0.149674	0.027935
-287.223	53.44883