Zajęcia 24

Estymacja MNW nieliniowych modeli SURE na przykładzie systemów wydatków

Zawartość tymczasowa i prowizoryczna.

1. Funkcja wiarygodności dla nieliniowego SURE, koncentracja

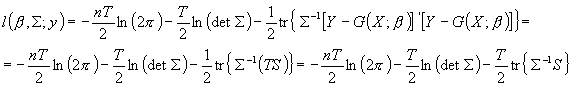
koncentrujemy po S:

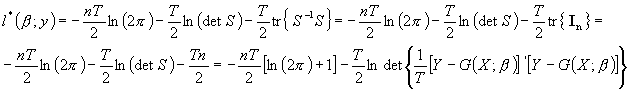
ostatecznie:

czyli:

Zakładamy tu, że S jest nieosobliwa; w przypadku układu z osobliwą macierzą S musimy przekształcić równania tak, by otrzymać nieliniowy układ SURE z nieosobliwą macierzą równoczesnych kowariancji.

2. ogólna charakterystyka systemów wydatków

w najprostszej wersji:

mamy n układ równań – opisujący popyt na n kategorii dóbr (dóbr zagregowanych):

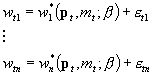
układ równań popytu w postaci udziałów, czyli:

-zmiennymi objaśnianymi są udziały wydatku na i-te dobro w wydatku całkowitym (mamy n takich równań dla wszystkich dóbr (w_ti to udział obserwowany (empiryczny) wydatku na i-te dobro w wydatku całkowitym dla obserwacji nr t)

-po prawej stronie mamy formę funkcyjną systemu popytu, czyli funkcję – udział teoretyczny; zależy ona od zmiennych objaśniających – dla każdego równania takich samych, tj. cen wszystkich n dóbr oraz wydatku całkowitego; oraz od parametrów. [w_i*(p_t m_t; b) to forma funkcyjna – udział teoretyczy; p_t to wektor n cen wszystkich dóbr; indeks i przy formie funkcyjnej udziału jest konieczny, bo w wydatku na każde kolejne dobro będą występowały także swoiste parametry]

Na parametry nakładamy rozmaite ograniczenia, ponieważ funkcja popytu musi spełniać różne własności. Źródła tych ograniczeń to m.in.

-wymóg sumowalności – wszystkie udziały teoretyczne muszą sumować się do jedności

-własności funkcji popytu:

– jednorodność stopnia zero względem cen i wydatku całkowitego łącznie (jeśli przemnożymy o stałą wszystkie ceny i wydatek całkowity to popyt się nie zmieni (przeliczenie pieniędzy ze złotych na grosze nie zmienia zakupionej ilości ani tym bardziej udziału wydatku na i-te dobro w wydatku całkowitym

– symetria Słuckiego – macierz Słuckiego musi być macierzą symetryczną; to warunek na funkcje elastyczności obserwowanego popytu.

Wymienione tu ograniczenia przekładają się na restrykcje równościowe wiążące parametry różnych równań które musimy narzucić w estymacji, więc musimy stosować estymację łączną (por zajęcia 23). Model jest nieliniowy, więc zostaje nam MNW z pełną informacją.

Przygotowanie zmiennych:

Jeżeli dysponujemy danymi o cenach dóbr i ilościach zakupionych:

Udziały empiryczne oraz wydatek całkowity tworzymy sztucznie z danych;

Aby wyliczyć wydatek obserwowany na i-te dobro mnożymy jego cenę razy ilość zakupioną

Aby wyliczyć obserwowany wydatek całkowity w danym okresie (m_t), sumujemy wydatki na wszystkie dobra

Aby wyliczyć udziały empiryczne wydatku na i-te dobro w wydatku całkowitym w okresie t, dzielimy uzyskany wcześniej wydatek na to dobro przez wydatek całkowity.

3. osobliwa macierz równoczesnych kowariancji, specyfikacja stochastyczna

Układ równań udziału danych powyżej musi się charakteryzować osobliwą macierzą równoczesnych kowariancji: udziały empiryczne i teoretyczne z konstrukcji sumują się do 1, więc równoczesne składniki losowe pełnego układu n równań muszą sumować się do zera. Czyli jeden z nich nie jest swobody (jest liniową kombinacją wszystkich pozostałych), czyli nie wszystkie są swobodne, czyli mają osobliwą macierz równoczesnych kowariancji (jest ona rzędu n-1 a nie n)

Musimy więc nasz układ sprowadzić do postaci z nieosobliwą macierzą równoczesnych kowariancji, mamy dwa sposoby:

A) zakładamy dla składników losowych rozkład normalny i wyrzucamy jedno równanie. A. Barten pokazał, że otrzymane oceny MNW parametrów są takie same bez względu na to które równanie pominiemy. Typowy t-ty wiersz Y oraz G to:

B) Zakładamy, że składniki losowe mają rozkład ALN (addytywny logistyczny normalny); odpowiada to przyjęciu standardowych addytywnych normalnych składników losowych w przekształconym układzie: rozpatrujemy w nim po lewej i po prawej stronie logarytmy ilorazów udziałów i-tego przez ostatni. Otrzymujemy tak n-1 równań (n-te byłoby bez sensu); w ostatnim (n-1)-szym mamy ln ilorazu udziału (n-1)-tego przez (n)-ty.

Typowy t-ty wiersz Y oraz G to:

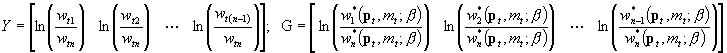
Porównanie specyfikacji:

Specyfikacja B jest bardziej spójna teoretycznie; ale jest gorsza numerycznie, bo w trakcie pracy algorytmu gdy tylko „wjedzie” on na takie parametry które w pewnym punkcie danych (udziały zależą od danych i to bardzo komplikuje sprawę) prowadzą do ujemnego udziału, mamy w Y logarytm liczby ujemnej i optymalizacja staje. Więc specyfikacja A charakteryzuje się znacznie lepszą zbieżnością; w B mamy problemy ze zbieżnością i ze znalezieniem punktów startowych; w skrajnej postaci możemy nawet zastosować specyfikację A tylko po to, by znaleźć punkty startowe dla B.

4. formy funkcyjne systemów wydatków

Będziemy praktycznie rozpatrywać dwie formy fukcyjne:

-linowy system wydatków (LES)

-system log-translog dla pośredniej funkcji użyteczności (LogTL)

LES:

Równanie udziału dla i-tego dobra w systemie LES ma postać:

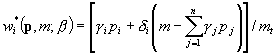; i = 1,...,n

mamy więc n parametrów d_i oraz n parametrów g_i. Interpretacja: do parametrów LES można opowiedzieć następującą „historyjkę”: dzielimy wydatek na „niezbędny” oraz „swobodny”; wtedy: g_i to ilości „niezbędne” każdego dobra; iloczyn g_ip_i to wydatek niezbędny na i-te dobro; w nawiasie okrągłym mamy „fundusz swobodnej decyzji” czyli wydatek całkowity minus suma wszystkich wydatków niezbędnych; parametry d_i to udziały wydatku na i-te dobro w funduszu swobodnej decyzji. W związku z tym (a także by zapewnić sumowanie udziałów teoretycznych do 1) parametry d_i sumują się do 1, czyli jeden z nich nie jest swobodny. W LES mamy więc de facto 2n-1 swobodnych parametrów.

Jedna mała uwaga: taka historyjka wymaga narzucenia na parametry restrykcji NIERÓWNOŚCIOWYCH – wszystkie muszą być nieujemne (bo „zakup niezbędny”, „udział” nie mogą być ujemne. W praktyce bywa, że g_i wychodzą ujemne. Co wtedy? Jeżeli jesteśmy bardzo przywiązani do „historyjki”, narzućmy restrykcje; tylko wtedy może być problem z własnościami estymatora i pogorszy się dopasowanie. Ale ta interpretacja parametrów nie jest „nieusuwalną” częścią LES – można ten system interpretować inaczej, więc w sumie nie musimy się tak zajmować restrykcjami dodatniości g_i. Dodatniość d_i jest bardziej podstawowa.

Elastyczności cenowe własne popytu na i-te dobro:

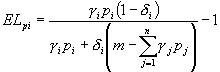
Elastyczności „dochodowe” popytu na i-te dobro:

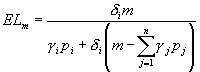
LogTL:

Równanie udziału systemu LogTL ma postać:

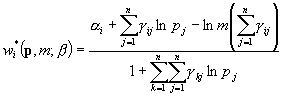
Zakładamy, że:

a)

oraz:

b)

(te warunki zapewniają sumowalność oraz symetrię Słuckiego; LogTL jest spełnia warunek jednorodności na mocy konstrukcji.

Zakładamy dodatkowo:

c) - ten warunek sprowadza system LogTL do klasy systemów w których (przy ustalonych cenach) udział teoretyczny jest liniową funkcją logarytmu wydatku całkowitego; taka własność jest pod pewnymi względami teoretycznie pożądana.

Ile parametrów ma system LogTL? Mamy n² parametrów g_kj oraz n parametrów a_j. Ile z nich jest swobodnych? Na mocy a) swobodnych jest (n-1) a_j; np. ostatnia a_n to 1 – suma pozostałych a_j.

Macierz parametrów g_kj jest na mocy b) symetyczna, czyli elementy np. nad przekątną (jest ich (n²-n)/2 są równe elementom pod przekątną.

Ponadto na mocy c) jeden element g_kj jest równy minus sumie pozostałych (najlepiej zastosować to do któregoś przekątniowego elementu g_jj.

Ostatecznie z n² + n parametrów (n²-n)/2+2 nie jest swobodnych.

Elastyczności cenowe własne popytu na i-te dobro:

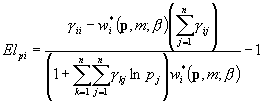
Elastyczności „dochodowe” popytu na i-te dobro:

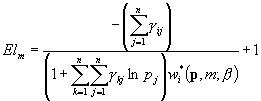
5. estymacja systemów wydatków

Dla celów estymacji musimy wyliczyć Y oraz G; żeby je mieć, musimy mieć udziały empiryczne i teoretyczne. Empiryczne wylicza się jak opisano wyżej. Teoretyczne wylicza się na podstawie formy funkcyjnej; ustalamy sobie wektor SWOBODNYCH parametrów danego systemu (po nich będziemy puszczać solver); następnie wyliczamy z nich wartości „nieswobodnych” parametrów; mając wszystkie parametry i zmienne objaśniające wyliczamy udziały teoretyczne. Muszą się sumować do jedności dla każdego t – jeśli tak nie jest, nie narzuciliśmy ograniczeń na parametry lub źle zakodowaliśmy formułę udziałów teoretycznych. Musimy oczywiście przyjąć jakieś początkowe wartości paramertów (punkty startowe) – o tym niżej.

Jak już mamy udziały empiryczne i teoretyczne, to:

-jeżeli stosujemy specyfikację stochastyczną A, to macierz Y robimy z (n-1) kolumn udziałów empirycznych, a G z tych samych (n-1) kolumn udziałów teoretycznych.

-jeżeli stosujemy specyfikację B, Y to (n-1) logarytmów ilorazów udziałów empirycznych typu ln[(i-ty <bez ostatniego>)/ostatni]; analogicznie tworzymy G, tylko z udziałów teoretycznych.

Wyliczamy z Y i G skoncentrowaną funkcję wiarygodności (UWAGA: za n przyjmujemy tyle, ile jest kolumn G lub Y, czyli (n-1) czyli ilość dóbr –1)

Następnie puszczamy „solver” po swobodnych parametrach aby maksymalizował funkcję wiarygodności.

Ze specyfikacją A będzie łatwiej.

PUNKTY STARTOWE:

LES: nie powinno być problemów. Za g_i można przyjąć zera, za d_i średni udział empiryczny dla i-tego dobra lub po prostu 0.33.

LogTL: w przypadku specyfikacji B sprawa się komplikuje; potrzebujemy takich punktów startowych żeby udziały były dodatnie i jeszcze się zbiegało. Można przyjąć a_j po około 0.33, a g_ik blisko zera. W ostateczności można zakodować dodatkową funkcję wiarygodności ze specyfikacją typu A (jak mamy udziały teoretyczne a i tak musimy je mieć to to jest pikuś), zmaksymalizować, i użyć takich wartości jako startowych w B (czyli przerzucić maksymalizację z powrotem na podstawową funkcję wiarygodności).

6. charakterystyki

Mając oszacowany system wydatków chcemy sobie jeszcze coś policzyć. W szczególności:

-miarę dopasowania do danych (tu będziemy stosować FIT Henri Theila)

-wartości charakterystyk ekonomicznych funkcji popytu na rozważane dobra, tj. elastyczności ze względu na wydatek całkowity (zwane dochodowymi) oraz ze względu na cenę własną. Spodziewamy się, że pierwsze będą dodatnie a drugie ujemne. Ale wychodzi różnie.

Jak wyliczyć FIT? Musimy mieć udziały empiryczne i teoretyczne, wtedy:

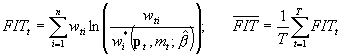
FIT_t to wartość wskaźnika FIT dla każdej obserwacji. Potem uśredniamy po obserwacjach. Powinno wyjść rzędu setnych-tysięcznych.

Pamiętajmy, żeby sprawdzić czy udziały (teoretyczne i empiryczne) sumują się do 1.

Interpretację FIT podawał Profesor: jest to miara rozbieżności między dyskretnymi rozkładami prawdopodobieństwa; jeden jest wyróżniany i traktowany jako wzorcowy (nie są traktowane symetrycznie). Tutaj wzorcowa jest obserwowana struktura konsumpcji i przymierzamy do niej teoretyczną strukturę konsumpcji. Dlaczego udziały możemy traktować jak rozkład dyskretny? Formalnie udziały mają te same własności (dodatnie sumują się do 1) co parametry rozkładu dyskretnego. Co do interpretacji, możemy powiedzieć, że rozkład ten reprezentuje prawdopodobieństwo opcji wyboru na które dobro wydamy losowo wybraną z naszych wydatków złotówkę.

ZADANIE:

Proszę oszacować na danych ds_data.xls LES ze specyfikacją A (z odrzucaniem jednego równania) oraz LogTL ze specyfikacją stochastyczną B (z logarytmami ilorazów).

Dla każdego z tych systemów proszę wyliczyć średnią wartość FIT oraz wartości elastyczności cenowej własnej i dochodowej dla każdego dobra w każdym punkcie danych. Elastyczności zilustrować na wykresach.

UWAGA!! W solverze proszę w „Opcjach” spróbować włączyć opcję „automatyczne skalowanie” i dać pochodne „centralne”.

Z ostatniej chwili: LogTL ze specyfikacją B jest rzeczywiście wredny. Trzeba do solvera dodać ograniczenie, że komórka w której jest minimalny udział teoretyczny jest większa od zera (czyli większa równa od jakiejś małej liczby). Mimo to są kłopoty – solver ograniczenie lekce sobie waży i nie chce się zbiegać nawet z punktów startowych wyliczonych ze specyfikacji A.

Jaka na to rada? Ja zrobiłem makro które losuje parametry z rozkładu normalnego z zadaną wariancją i z wartością oczekiwaną równą wartościom parametrów ze specyfikacji A; ale rozumiem że nie każdy ma na to ochotę. Podaję więc uzyskane przeze mnie punkty startowe (2 zestawy) z których LogTL ze specyfikacją B powinien się zbiegać mimo wszystko:

PUNKTY STARTOWE LogTL

a1	0.070932	0.048217
a2	0.568435	0.561308
g11	0.218712	0.122192
g21	-0.14921	-0.10975
g31	-0.09136	-0.0431
g22	0.403725	0.516114
g32	-0.25503	-0.39836

Jeżeli ktoś nie uzyska mimo to zbieżności logTL ze specyfikacją B, proszę zrobić z A, za to LES z B.

Wyniki dla sprawdzenia:

LogTL:

	spec. A		spec. B
	FIT śr		FIT śr
	0.000369		0.000371
	ln L		lnL
	308.7728		156.7449
a1	0.095811	a1	0.130298
a2	0.619369	a2	0.600668
g11	0.151891	g11	0.120564
g21	-0.07613	g21	-0.05333
g31	-0.0816	g31	-0.06819
g22	0.478239	g22	0.458564
g32	-0.36879	g32	-0.3746

LES:

Tu nie było problemów; specyfikacja A działa jeżeli startowo przyjmie się gammy równe 0 oraz delty równe 1/3. uzyskane ze specyfikacji A parametry można wykorzystać (i działają) jako punkty startowe dla specyfikacji B

Wyniki:

	A		B
	FIT śr		FIT śr
	0.0016502		0.001566
	ln L		lnL
	226.11477		78.4602
g1	14.280497	g1	7.091958
g2	64.736661	g2	43.53471
g3	-19.2792	g3	-61.8987
d1	0.1353953	d1	0.133397
d2	0.3572702	d2	0.354687