Na tej stronie będą zebrane różne przydatne fakty z algebry macierzowej. Na razie jest prowizorka i bałagan, ale może z czasem się ułoży.

Algebra macierzowa

PEWNE WAZNE OPERACJE MACIERZOWE

¢ oznacza transpozycję macierzy.

(A¢)¢ = A, dla macierzy symetrycznej: A¢ = A

skalar A = [a₁₁] [macierz (1 ´ 1)] jest zawsze symetryczny: [a₁₁] = [a₁₁]¢

Dla n-wymiarowego wektora kolumnowego x:

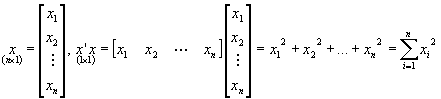
x¢x (wiersz razy kolumna) to skalar - suma kwadratów elementów wektora x.

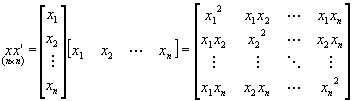
xx¢ (kolumna razy wiersz) to macierz symetryczna stopnia n zawierająca w i-tym wierszu i j-tej kolumnie iloczyny par x_ix_j

dla n-wymiarowego wektora i zawierającego tylko jedynki:

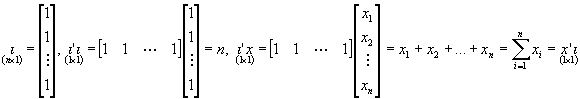
dla n-wymiarowego wektora a:

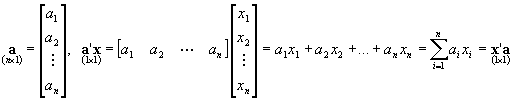
dla n-wymiarowych wektorów kolumnowych a, b : a¢b = b¢a ; ab¢ = ba¢

WYZNACZNIK MACIERZY, RZĄD MACIERZY, MACIERZ ODWROTNA

Wyznacznik macierzy [ozn. det(A) ] to skalarna funkcja macierzy kwadratowej.

Jeżeli A jest macierzą (1 ´ 1) , tj. A = [a₁₁], do det(A) = a₁₁

Dla macierzy (2 ´ 2),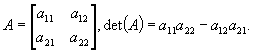

Dla macierzy (3 ´ 3) można wyliczyć wyznacznik następująco:

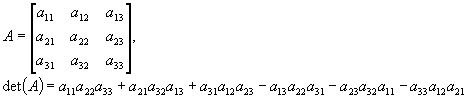
Macierz odwrotna do macierzy kwadratowej A (stopnia n) - jeżeli istnieje - to macierz również kwadratowa stopnia n (ozn. A^-1), mająca własność:

A^-1A = A A^-1 = I

Macierz odwrotna jest wyznaczona jednoznacznie.

Macierz odwrotna istnieje dla macierzy tzw. nieosobliwych, czyli mających własność det (A) ¹ 0.

Aby wyliczyć macierz odwrotną do pewnej danej macierzy A, możemy posłużyć się metodą dopełnień

(do odwracania macierzy stopnia 2,3).

Kroki w tej metodzie są następujące:

1. Wyliczamy macierz dopełnień D o typowym elemencie (w i-tym wierszu i j-tej kolumnie):

d_ij = (-1)^i+j M_ij

gdzie M_ij to wyznacznik macierzy powstałej przez wykreślenie z A i-tego wiersza i j-tej kolumny.

2. Wyliczamy wyznacznik macierzy A , czyli det(A) – żeby macierz dało się odwrócić, musi wyjść różny od zera. Mając macierz dopełnień, możemy wyliczyć det(A) wybierając dowolny wiersz lub kolumnę D,i mnożymy przez odpowiedni wiersz (kolumnę) macierzy A „element po elemencie”):

co może być szybsze niż metody podane wyżej, kiedy już mamy D.

3. Wyliczamy ostatecznie:

czyli: 1/(wyznacznik A) razy macierz dopełnień TRANSPONOWANA (o czym łatwo zapomnieć).

Rząd macierzy (niekoniecznie kwadratowej) A [ ozn. rz(A) ] to stopień największego niezerowego podwyznacznika powstałego przez wykreślenie dowolnych kolumn / wierszy A. Jest to maksymalna liczba liniowo niezależnych kolumn (wierszy) macierzy A. Oczywiście rząd nie może być większy od mniejszego wymiaru macierzy. Rząd jest zerowy gdy macierz zawiera wyłącznie zera.

Rozmaite własności macierzy (zakładając że wszystkie działania da się wykonać):

1. (AB)¢ = B¢A¢ ; (ABC)¢= C¢B¢A¢

2. (AB) ^-1 = B^-1 A^-1 ; (ABC) ^-1 = C^-1 B^-1 A^-1

3. rz (AB) £ min [ rz(A), rz(B) ]

4. rz (B¢B) = rz (BB¢) = rz (B)

5. det(CD) = det(C) det (D)

Dla macierzy kwadratowej A (n ´ n) , jeśli Az = 0 dla pewnego wektora z ¹ 0, to det(A) = 0.

Dla macierzy X (T ´ k), jeśli Xz = 0 dla pewnego wektora z ¹ 0, to kolumny macierzy X nie są liniowo niezależne, więc rz(X) < k. Jeśli rz(X) = k, to rz(X¢X) = k więc det(X¢X) ¹ 0,

i nie istnieje z ¹ 0 taki, że (X¢X)z = 0.

FORMY KWADRATOWE; OKREŚLONOŚĆ MACIERZY

Dla symetrycznej macierzy A stopnia n rozważamy funkcję n-wymiarowego wektora kolumnowego x o postaci:

f_A(x) = x¢Ax

zwaną formą kwadratową.

Przykład: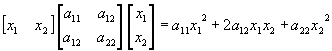

Kryterium określoności macierzy jest znak formy kwadratowej dla DOWOLNEGO niezerowego x:

Jeżeli to macierz A jest dodatnio określona

Jeżeli to macierz A jest ujemnie określona

Jeżeli to macierz A jest dodatnio półokreślona

Jeżeli to macierz A jest ujemnie półokreślona

Jeżeli A jest dodatnio określona lub dodatnio półokreślona, mówimy, że jest nieujemnie określona.

Jeżeli A jest ujemnie określona lub ujemnie półokreślona, mówimy, że jest niedodatnio określona.

Każda macierz dodatnio półokreślona lub ujemnie półokreślona jest osobliwa – jej wyznacznik jest zerowy, ponieważ skoro x¢Ax = 0 dla niezerowego x, to Ax = 0 => kolumny A nie są liniowo niezależne, więc det(A) = 0.

Przykład:

Dla macierzy F (n ´ m) rozważmy określoność macierzy symetrycznej A = F¢F (n ´ n). Forma kwadratowa z niezerowym wektorem x ma tu postać:

f _F¢F (x) = x¢Ax = x¢ F¢F x = (Fx)¢Fx = c¢c dla wektora c = Fx,

ponieważ c¢c = (c₁² + c₂² +...+ c_n²) to suma kwadratów, jest zawsze nieujemna. Skoro tak, macierz F¢F jest nieujemnie określona dla dowolnego F (na mocy konstrukcji). Ta forma kwadratowa może przybierać wartość zerową dla niezerowego x wtedy i tylko wtedy, gdy Fx = 0, co implikuje rz(F)<m. Jeśli rz(F) = m, Fx ¹ 0 i forma kwadratowa przyjmuje tylko wartości dodatnie, więc F¢F jest dodatnio określona, gdy rz(F) = m. Zastosowanie: w dowodzie twierdzenia Gaussa-Markowa macierz nieujemnie określoną zapisujemy F¢F. Dla X spełniającego założenia KMRL, X¢X jest dodatnio określona, co przydaje się np. w wykazaniu że estymator MNK minimalizuje sumę kwadratów reszt.

POCHODNE CZĄSTKOWE FUNKCJI WIELU ZMIENNYCH w NOTACJI MACIERZOWEJ

Dla y = f(x) - różniczkowalnej rzeczywistej funkcji k zmiennych (k-wymiarowego wektora x) rozważamy k-wymiarowy wektor pierwszych pochodnych (gradient) i macierz kwadratową stopnia k drugich pochodnych (Hessian), w notacji macierzowej:

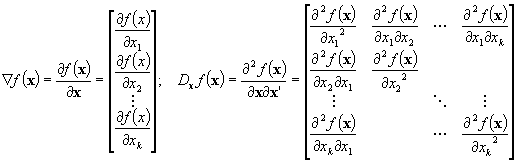
przykłady:

dla k-wymiarowego wektora a, kwadratowej macierzy A stopnia k,

(to tylko stwierdzenie faktu, że pochodna cząstkowa funkcji liniowej a₁x₁+ a₂x₂+...+ a_kx_k kolejno po x₁, x₂ to kolejno a₁, a₂ ...)

z kolei pochodne formy kwadratowej przyjmują postać:

OPTYMALIZACJA FUNKCJI WIELU ZMIENNYCH

Warunkiem koniecznym istnienia ekstremum lokalnego różniczkowalnej funkcji w punkcie x^(*) jest zerowanie się w tym punkcie wektora pierwszych pochodnych cząstkowych (gradientu) . Dodatkowym warunkiem wystarczającym by optimum było globalne, jest by funkcja była wklęsła (wypukła) – co zależy od określoności macierzy drugich pochodnych cząstkowych (Hessianu). Jeśli ta macierz jest dodatnio określona dla każdego x, znaleziony punkt zerowania gradientu x^(*) to minimum; jeśli ujemnie określona – to maksimum.

Przykład: badanie funkcji f(x) = c + a¢x + x¢Bx (gdzie wektory c, a oraz macierz symetryczna B=B¢ to pewne stałe).

Zauważmy, że określoność Hessianu jest taka sama jak określoność macierzy B i jest taka sama dla każdego x; warunkiem wystarczającym dla istnienia ekstremum w punkcie x^(*) (minimum lub maksimum, to zależy od określoności B) jest zerowanie gradientów, więc by 2Bx^(*) = -a.

Przykład , rozwinięcie: zbadajmy ekstremum sumy kwadratów reszt MNK jako funkcji b:

S(b) = y¢y – 2y¢Xb+b¢X¢Xb

S(b) to funkcja wektora b z parametrami y oraz X,

ta funkcja to szczególny przypadek f(x) = c + a¢x + x¢Bx

Tutaj składnik y¢y nie zależy od b więc można go pominąć, wektor – 2y¢X to a¢ zaś X¢X to B.

Badamy pierwsze pochodne:

,

więc warunek zerowania pierwszych pochodnych ma postać (X¢X)b = X¢y

[zauważmy, że w f(x) występuje a¢, natomiast w pochodnej a = (a¢) ¢ , więc w pochodnej y¢X przechodzi w X¢y ].

Warunek wystarczający globalnego ekstremum sprowadza się do zbadania określoności (X¢X):

,

która jest taka sama dla dowolnego b, bo nie zależy od b.

powyżej pokazano, że (X¢X) jest dodatnio określona gdy rz(X) = k.

Ostatecznie warunek minimalizacji sumy kwadratów reszt ma postać:

(X¢X)b = X¢y

co prowadzi do wzoru na estymator MNK (por. Zajęcia 2)

Warunki określoności macierzy:

Kryterium wyznacznikowe:

Wiodący minor główny stopnia k (leading principal minor of order k) macierzy A to wyznacznik podmacierzy stopnia k obejmującej elementy od a₁₁ do a_kk. Macierz kwadratowa stopnia n ma n wiodących minorów głownych. Oznaczamy je przez M_k(A).

Przykład:

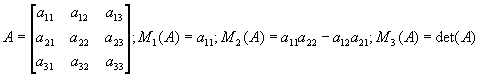
Formę kwadratową opartą na macierzy A można przedstawić następująco:

gdzie dokładna postać niezerowego wyrażenia (...) nie jest istotna. Ta reprezentacja wyraźnie sugeruje, że warunkiem koniecznym i wystarczającym dodatniej określoności macierzy A (czyli dodatniości formy kwadratowej dla dowolnego niezerowego x) jest dodatniość wszystkich n wiodących minorów głównych macierzy A. Wobec tego wyznacznik macierzy dodatnio określonej jest zawsze dodatni.

Warunkiem koniecznym i wystarczającym ujemnej określoności A jest, by M₁(A) był ujemny, a kolejne minory M₂(A), M₃(A) itd. zmieniały znak (czyli M₂(A) był dodatni, M₃(A) ujemny itd.)

Warunki wyznacznikowe półokreśloności są bardziej złożone i nie będą tu przedstawiane.

Kryterium wykorzystujące wartości własne:

Macierz A jest dodatnio określona Û wszystkie jej wartości własne są dodatnie.

Macierz A jest ujemnie określona Û wszystkie jej wartości własne są ujemne.

Macierz A jest dodatnio półokreślona Û wszystkie jej wartości własne są nieujemne i przynajmniej jedna jest równa 0.

Macierz A jest ujemnie półokreślona Û wszystkie jej wartości własne są niedodatnie i przynajmniej jedna jest równa 0.

Macierz kwadratowa stopnia n ma n wartości własnych. Wartości własne macierzy symetrycznej są zawsze rzeczywiste.

Kryterium wartości Cholesky’ego.

Niech L będzie macierzą trójkątną dolną jednostkową (tzn. taką, która ma zera ponad przekątną oraz jedynki na przekątnej. Niech D będzie macierzą diagonalną (mającą zera poza przekątną).

Każda macierz A dodatnio (pół)określona ma tzw. reprezentację Cholesky’ego o postaci:

A = L’DL

Dekompozycja Cholesky’ego macierzy dodatnio określonej jest jednoznaczna.

Elementy na przekątnej macierzy D to wartości Cholesky’ego.

Twierdzenie: Jeżeli reprezentacja symetrycznej macierzy A w postaci Cholesky’ego istnieje, to liczba dodatnich ujemnych i zerowych wartości Cholesky’ego jest równa liczbie odpowiednio dodatnich, ujemnych i zerowych wartości własnych. Wobec tego:

Aby sprawdzić [narzucić] dodatnią określoność (półokreśloność) macierzy, wystarczy sprawdzić [narzucić] dodatniość (nieujemność) jej wartości Cholesky’ego.

Aby narzucić ujemną określoność macierzy A, wystarczy i potrzeba narzucić dodatnią określoność macierzy –A.

Źródło: Lawrence J. Lau Testing and imposing monoticity, convexity and quasi-convexity constraints.

ILOCZYN KRONECKERA

Iloczyn Kroneckera AÄB przemnaża każdy element A przez całą B i buduje z tego taką dużą macierz:

Przykład 1:

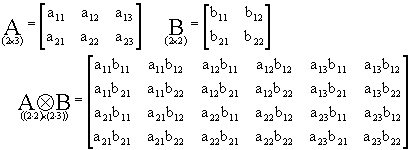
Przykład 2:

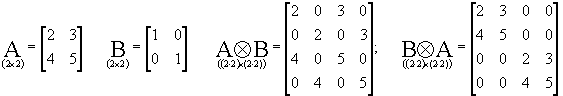
WŁASNOŚCI ILOCZYNU KRONECKERA:

1) (AÄB)(CÄD) = ACÄBD

2) (AÄB)^-1=A^-1ÄB^-1

3) (AÄB)’= A’ÄB’

4) AÄ(B+C) = AÄB + AÄC

5) (B+C) Ä A = BÄA + CÄA

6) det(AÄB) = det(Aⁿ)det(B^m) (tu det() oznacza wyznacznik, macierz A jest m´m, B n´n (potęgi odwrotnie))

7) tr(AÄB) = tr(A)tr(B) ( tr( ) to ślad macierzy czyli suma elementów na głównej przekątnej)

8) rz(AÄB) = rz(A)rz(B)

(powyżej zakładamy, że wszystkie zwykłe iloczyny macierzy i odwrócenia dają się wykonać)

oczywiście iloczyn Kroneckera nie jest przemienny

Jak widać iloczyn Kroneckera posiada mnóstwo magicznych własności. Radzę się ich nauczyć NA PAMIĘĆ i poćwiczyć bo się bardzo przydadzą.