Zajęcia
10
Analiza procesu
produkcyjnego II: Specyfikacja stochastyczna, dynamizacja. Funkcja
translogarytmiczna.
Podsumowanie zajęć poprzednich / Wprowadzenie
Na poprzednich zajęciach wprowadzona została mikroekonomiczna funkcja produkcji oraz dwie formy funkcyjne. Na dzisiejszych zajęciach przedstawione zostanie zagadnienie specyfikacji stochastycznej i estymacji funkcji produkcji. Pokazany zostanie prosty sposób wprowadzania dynamiki do modelu dla danych w postaci szeregów czasowych. Przedstawiona zostanie ponadto translogarytmiczna funkcja produkcji jako przykład nowoczesnej formy funkcyjnej.
Zajęcia 10
Celem zajęć jest przedstawienie podstawowej
specyfikacji stochastycznej dla funkcji produkcji; prezentacja modelu
translogarytmicznej formy funkcyjnej oraz jej estymacja w postaci statycznej i
zdynamizowanej.
Specyfikacja
stochastyczna i estymacja
Dla celów estymacji nakłada się na deterministyczną formę funkcyjną technologii (funkcji produkcji) czynnik (bo go nie dodajemy – jak składnika) losowy:
(1) 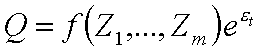
(o et przyjmuje się założenia takie jak w KMRL lub KMNRL). Taka specyfikacja zamiast prostego addytywnego składnika losowego o postaci:
(2) ![]()
posiada kilka zalet.
W przypadku (2) wahania losowe wielkości produkcji przeciętnie wynoszą s jednostek (niezależnie od skali produkcji). W przypadku (1) wahania losowe są proporcjonalne do skali produkcji – jeśli e jest około 0, to teoretyczną wielkość produkcji mnożymy razy ee, czyli około 1. Zakłócenia losowe wynoszą więc mniej więcej tyle samo procent wielkości produkcji, a nie tyle samo jednostek, jak w (2). Wydaje się nam to intuicyjnie bardziej uzasadnione i zbliżone do prawdziwych własności procesu produkcyjnego.
Specyfikacja (2) nie zapewnia także, że obserwowana wielkość produkcji będzie zawsze dodatnia. Teoretycznie możliwa jest tu sytuacja wylosowania się silnie ujemnego epsilona, co mogłoby odpowiadać obserwowaniu ujemnej produkcji, czego nie potrafimy zinterpretować. W specyfikacji (1) obserwowana wielkość produkcji musi być dodatnia, bo produkcja teoretyczna jest mnożona razy ee, czyli liczbę większą lub mniejszą od 1, ale zawsze większą od zera.
Ponadto w specyfikacji (1) konieczne jest zlogarytmowanie równania – w celu doprowadzenia go do postaci ze składnikiem losowym (czyli z ...+ et). Po zlogarytmowaniu wiele form funkcyjnych (Translog – patrz niżej, CD) sprowadza się do postaci liniowej względem parametrów. Oznacza to większą prostotę estymacji – dla realizacji nie jest potrzebny algorytm numeryczny którego realizacja może nastręczać trudności, a wystarczy wzór analityczny, który daje się prosto wyliczyć. Dodatkowo, w modelach liniowych dysponujemy lepszymi własnościami technik wnioskowania – modele nieliniowe odwołują się do aproksymacji asymptotycznej, własności technik wnioskowania w małej próbie nie są znane, a w modelach liniowych znamy własności małopróbkowe. Ogólnie, modele nieliniowe odwołują się do jednego przybliżenia więcej w porównaniu z modelami nieliniowymi.
Widzimy więc, że wybór specyfikacji stochastycznej może być dyktowany zarówno dążeniem do osiągnięcia jak najlepszej zgodności z tym, jak rozumiemy prawdziwe własności modelowanego procesu (wahania losowe proporcjonalne do skali), jak i względami praktycznymi (dążeniem do postaci liniowej gdzie łatwiej uzyskać oceny parametrów) lub teoretycznymi, ale związanymi z własnościami procedur wnioskowania (w modelach liniowych mamy własności małopróbkowe, „dokładne”). Zwykle wszystkie te aspekty występują łącznie.
Po zlogarytmowaniu (1) otrzymujemy:
(3) ![]()
Ta postać będzie podstawą estymacji. Przykładowo gdy przyjmiemy formę funkcyjną C-D otrzymamy:
(4) ![]()
Zauważmy, że (4) może spełniać założenia KMRL/KMNRL.
Przypominam uwagę z zajęć poprzednich: zakładamy tu deterministyczną funkcję produkcji – składnikowi losowemu nie nadajemy interpretacji ekonomicznej. Są inne podejścia.
Specyfikacja dynamiczna (tylko dla szeregów czasowych)
Dla danych w postaci szeregów czasowych rozpatruje się dynamizację funkcji produkcji poprzez np. wprowadzenie do niej explicite funkcji czasu (numeru okresu). Może to odpowiadać oddziaływaniu postępu techniczno-organizacyjnego. Prosty sposób dynamizacji to modyfikacja (1) do postaci:
(5) ![]()
poprzez wprowadzenie dodatkowego parametru t [tau] (zmienna t to numer okresu odpowiadającego obserwacji). Wtedy (3) przyjmuje postać:
(6) ![]() .
.
Wartość parametru tau możemy interpretować następująco: z okresu na okres przy niezmienionych nakładach wielkość produkcji rośnie/spada o (t*100%) wyłącznie na skutek zmian techniczno-organizacyjnych [postępu, jeśli tau jest dodatnie, i regresu, jeśli ujemne]. Wartość tau wynosząca 0,03 oznacza, że z okresu na okres wielkość produkcji rośnie o około 3% wyłącznie na skutek postępu techniczno-organizacyjnego.
Interpretacja taka wynika z opisanego w Zajęciach 3 przypadku, gdy zmienna objaśniana jest logarytmem pewnej wielkości ekonomicznej, a zmienna objaśniająca wprost jest wielkością ekonomiczną. Wtedy dla bliskich zeru wartości parametrów możemy stosować taką interpretację jak opisano powyżej. W praktyce spodziewamy się właśnie bliskich zeru ocen parametru t. Gdybyśmy jednak otrzymali większą co do wartości bezwzględnej ocenę i chcieli ją interpretować, trzeba byłoby powiedzieć, że „... wielkość produkcji wzrośnie o około (1-et)*100%”.
Kiedy do funkcji produkcji wprowadzamy dynamizację, faktycznie rozpatrujemy już funkcję produkcji o postaci:
(7) ![]()
co trzeba uwzględnić w wyprowadzeniach i interpretacji. Przykładowo dla zdynamizowanej funkcji CES produkcyjność krańcowa przyjmie postać:
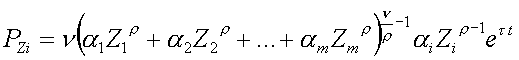
w interpretacji (ponieważ produkcyjność krańcowa jest tu funkcją t) należy dodać słowa „w okresie t=...”. Z kolei w formule dla elastyczności zdynamizowanej funkcji CES czynnik ett uprości się, ponieważ produkt krańcowy dzielimy przez Q które też zawiera ett. Wobec tego w interpretacji elastyczności numeru okresu już nie uwzględniamy; podobnie będzie w przypadku TSS. Podobnie będzie w przypadku innych form funkcyjnych – w interpretacji numer okresu musimy wymienić dla produkcyjności krańcowych.
UWAGA! Jeśli mamy do czynienia ze zdynamizowaną funkcją produkcji, to wszystkie typowe interpretacje (np. efektu skali, elastyczności itd.) zakładają niezmienność t – więc w przypadku funkcji produkcji z dynamizacją i charakterystyk innych niż produkcyjności krańcowe, dla w pełni poprawnej interpretacji, powinniśmy dodać „przy niezmienionym t”, lub ładniej „w danym okresie”, czy „w tym samym okresie” – wiec np. przy interpretacji efektu skali można powiedzieć coś takiego: „gdyby nakłady wszystkich czynników produkcji wzrosły o 1% w pewnym okresie, to wielkość produkcji w tym okresie wzrosłaby o około x%”. (to w funkcji CES lub C-D).
Funkcja
Translog. Giętkie formy funkcyjne
Pokazane dotąd formy funkcyjne wyznaczają pewne etapy historycznego rozwoju ekonometrycznej analizy procesu produkcyjnego. Funkcja C-D to tak mniej więcej lata 20; funkcja CES – lata 50 – to przybliżone daty „powstania”. Zauważmy, że funkcja CES znosi niektóre ograniczenia nakładane przez formę C-D: w funkcji CES elastyczności zależą od nakładów (co prawda nie w sposób swobodny, bo cały czas się muszą sumować do n); ponadto elastyczność substytucji może podlegać szacowaniu (a nie wynosi 1, jak w C-D). Jednak zastanawiano się, czy ograniczenia teoretyczne narzucane przez funkcję CES nie są i tak zbyt silne – poszukiwano modelu, który lepiej pozwoli „przemówić danym” – dostarczyć nam lepszą wiedzę o kształtowaniu się nieznanych charakterystyk technologii.
W zajęciach 6 pokazywaliśmy, jak można rozszerzyć możliwości modelu liniowego poprzez wprowadzenie do niego nieliniowych kombinacji kilku wielkości ekonomicznych. Uzyskiwaliśmy tak model, który pozwalał na odwzorowanie subtelnych i skomplikowanych zależności między badanymi wielkościami ekonomicznymi – choć nasze uzasadnienie było nieformalne, heurystyczne.
Idąc w tym kierunku, w latach 70 rozwinięto podejście opierające się na tzw. giętkich formach funkcyjnych (Flexible functional forms, FFF). „Giętkość” rozmaicie się definiuje – zaproponowano wiele sposobów jej określenia – dlatego tutaj tylko zarysujemy nieformalnie ideę stojącą za jedną z interpretacji. Ogólnie jednak cel wprowadzenia FFF jest taki: jak najlepiej odwzorować pewną nieznaną funkcję. Nieznana funkcja (w naszym przypadku „prawdziwa” funkcja produkcji) to funkcja aproksymowana (przybliżana), stosowana zaś do jej badania (giętka) forma funkcyjna to funkcja aproksymująca. Otóż rozważmy taką funkcję aproksymującą, która jest w stanie odwzorować nieznaną funkcję aproksymowaną w pewnym punkcie dziedziny z dokładnością do drugich pochodnych włącznie. Co to znaczy „.. do drugich pochodnych włącznie” – to znaczy, że „w pewnym punkcie” funkcja aproksymująca ma: tę samą wartość (funkcji), te same wartości I-szych i II-ich pochodnych co funkcja aproksymowana. O co chodzi z „pewnym punktem”? to taki rodzaj argumentu. My nie wiemy, który to punkt; potrzebujemy dobrego odwzorowania w wielu punktach – np. we wszystkich punktach danych. Definicja nam tego nie gwarantuje, ale powtarzam: ta definicja to tylko rodzaj argumentu, pewien sposób na porównywanie zdolności form funkcyjnych do odwzorowania nieznanych funkcji. Przedstawione tu rozumienie giętkości to tzw. lokalna giętkość (bo rozważamy „pewien punkt”); sposób rozumienia dokładności odwzorowania przez odzwierciedlenie wartości pochodnych to tzw. giętkość w sensie Diewerta. W. Erwin Diewert to człowiek który bardzo dużo zrobił dla teorii giętkich form funkcyjnych. Poniżej przedstawimy pewną (znakomitą – jak dowiodło jej szerokie zastosowanie) propozycję lokalnie giętkiej formy funkcyjnej – czyli funkcję translogarytmiczną – ale to niejedyna taka forma.
Laurits R. Christensen, Dale W. Jorgenson i Laurence J. Lau przedstawili propozycję transcendentalnej-logarytmicznej formy funkcyjnej (transcendental-logarithmic) nazwaną w skrócie Translog. Po lewej stronie mamy w niej logarytm naturalny objaśnianej wielkości, a po prawej stronie funkcję kwadratową w logarytmach wielkości objaśniających. Można to krótko zapisać macierzowo.
Załóżmy, że chcemy modelować funkcję:
![]()
gdzie x jest wektorem argumentów (wielkości objaśniających); wtedy funkcja translog przyjmie postać:
(8) ![]()
gdzie:
z to wektor logarytmów x
a parametry są podzielone między a0, a,B:
a0 to skalar,
a to wektor tego wymiaru co x czy z
B to macierz kwadratowa
i symetryczna (B=B’)
0,5 to wynik pewnej normalizacji – nie zmienia istoty sprawy.
Kiedy rozpiszemy sobie (8) okaże się, że objaśniamy ln y poprzez: wyraz wolny, logarytmy x-ów oraz iloczyny (mieszane i kwadraty) par logarytmów x-ów. Dla przykładu, rozważmy dwuczynnikową funkcję produkcji z nakładami K i L (kapitał i praca), wtedy funkcja Translog przyjmie postać:
(9) ![]()
w (9) w porównaniu z (8)
Q to y
a = [a1 a2]¢
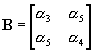
x to [K L]'
z to [lnK lnL]'
(co można sobie łatwo sprawdzić bezpośrednim rachunkiem)
Uwaga: obecność w (9) stałych (0.5) lub jej brak nie zmienia zasadniczych wartości funkcji translog – nie trzeba się więc do nich zbytnio przywiązywać. Trzeba tylko być konsekwentnym i w całym rachunku trzymać się jednej postaci i spójnych oznaczeń. Dlatego możemy rozpatrywać funkcję:
(10) ![]()
a jak ktoś się doczepi, to nasze a3 i a4 to funkcje oryginalnych parametrów i w każdej chwili możemy wrócić do tamtych.
(czasem (lnK)2 zapisuje się ln2K – zaznaczamy, ze chodzi o kwadrat całego logarytmu, bo gdyby to był kwadrat K, to 2 spadłaby przed logarytm i (10) nie dałoby się oszacować z powodu zbyt niskiego rzędu X)
Rozważmy, jaką postać przyjmują charakterystyki procesu produkcyjnego w funkcji translog – dla uproszczenia rozważymy dwuczynnikową funkcję w postaci (10).
Najwygodniej będzie zacząć od elastyczności, bo (10) aż się prosi o pochodną logarytmiczną:
![]()
![]()
![]()
Produkcyjności krańcowe można wyliczyć podstawiając Q = exp(lnQ) według (10) do odpowiedniego wzoru z zajęć 9 podobnie, TSS możemy wyliczyć korzystając z wzoru z elastycznościami, uzyskując:
produkcyjność krańcową kapitału jako ![]()
(jeśli funkcja jest zdynamizowana, to produkcyjność krańcowa zależy od t poprzez Q)
TSS jako ![]()
(w TSS Q się upraszcza,
więc jeśli mamy w modelu dynamizację, to ta charakterystyka nie zależy od t – w
interpretacji nie musimy więc dodawać „dla t = ..”., a tylko „w danym
okresie”, ponadto widzimy, że zależy ona nie tylko od ilorazu nakładów, ale
od poziomów nakładów (poprzez elastyczności) – więc ponieważ przy takim samym
stosunku nakładów ale innych poziomach TSS może mieć inną wartość, to w
interpretacji musimy zaznaczyć ile wynoszą poziomy nakładów (a nie jaki jest
ich stosunek, jak przy TSS w funkcji C-D lub CES)).
Przykład: jeśli w
zdynamizowanej dwuczynnikowej funkcji translog (nakłady K i L) otrzymamy
wartość RLK = 1,5 to interpretujemy np. tak:
W danym okresie, gdy chcemy utrzymać niezmienioną
wielkość produkcji, jedna jednostka nakładu kapitału zastępuje około 1,5
jednostki nakładu pracy, przy nakładach pracy i kapitału odpowiednio na
poziomach K*=...,L*=... .
Podsumowując, dla nas ważne jest, że widzimy: w funkcji translog WSZYSTKIE charakterystyki są funkcjami WSZYSKICH nakładów, więc możemy badać empirycznie zmienność wszystkich charakterystyk przy różnych kombinacjach nakładów. W zadaniach, do celów obliczania TSS i Pzi możemy sobie wyliczyć wartość Q* i podstawiać liczbę; co do interpretacji, to już wiemy, że przy WSZYSKICH charakterystykach funkcji translog w interpretacji musimy umieścić poziomy wszystkich nakładów: np. RTS:
Wielkość produkcji wzrośnie o <RTS> % jeśli nakłady wszystkich czynników wzrosną jednocześnie o 1 procent odpowiednio z poziomu K*, L*.
(to dla (10) gdzie K i L to wszystkie czynniki)
poziom nakładów musimy zaznaczyć, bo przy innym poziomie RTS jest inny i interpretacja nie byłaby prawdziwa. Ponadto nie uwzględniamy tu dynamizacji.
Takie trochę
bardziej zaawansowane rozważania
Fakt, że w funkcji translog wszystkie charakterystyki są funkcją wszystkich nakładów jest dla nas bardzo ważny. Sprawia to, że możemy badać np. zależność efektu skali od poziomu nakładów, co w funkcji C-D i CES nie jest możliwe. W C-D i CES efekt skali jest niezależny od nakładów – czyli globalny w przestrzeni nakładów [taki sam dla dowolnego wektora Z = (Z1,..,Zm)’]; podobnie elastyczności w funkcji C-D i ES w funkcji CES (o CD nie wspominając). W funkcji translog rozważane charakterystyki są lokalne w przestrzeni nakładów – czyli zależą od wektora nakładów Z = (Z1,..,Zm)’. Elastyczności w CES też są lokalne, ale nie są swobodne, bo muszą się sumować do globalnego RTS – czyli wzrost jednej elastyczności wymusza taki sam spadek drugiej (dla dwuczynnikowej CES). Podsumowując – w CD elastyczności są globalne, w CES lokalne ale nie swobodne, w Translog lokalne i swobodne.
Podobnie elastyczność substytucji w funkcji CES jest globalna – niezależna od nakładów; dla każdej pary nakładów taka sama (por. wzór); jest to problem gdy występuje więcej czynników produkcji – funkcja CES wymusza taką samą substytucyjność dla wszystkich rozważanych par nakładów (czyli dla pracy energii kapitału praca i kapitał MUSZĄ się dawać zastępować tak samo łatwo lub tak samo trudno jak praca i energia oraz kapitał i energia). Wobec tego dla więcej niż 2 nakładów f. CES jakoś uśredni relację między nimi. Wnioskujemy stąd, że dla badania zastępowalności (substytucyjności) czynników produkcji funkcja C-D nie nadaje się w ogóle (bo narzuca pewien typ substytucyjności odpowiadający ES = 1 niezależnie od danych); funkcja CES może się nadawać ale co najwyżej dla 2 czynników (zauważmy, że ES będzie globalna, ale przynajmniej będzie podlegać szacowaniu); natomiast funkcja Translog pozwala na względnie swobodne i lokalne kształtowanie się ES (wzór wyjdzie dość pokręcony [można też korzystać z pochodnej logarytmicznej] , ale wyjdzie) – więc względnie najswobodniej odzwierciedla „prawdziwą” strukturę.
Widzimy, że funkcja translog rzeczywiście „pozwala danym przemówić”. Jaka jest za to cena? (bo zawsze jest cena J)
Otóż w funkcji translog mamy problemy z regularnością ekonomiczną czyli ze spełnieniem warunków stawianych funkcji produkcji. Dla CES i C-D omawiane ograniczenia na parametry (por. zajęcia 9) zapewniają regularność globalną – dla dowolnego dozwolonego (dodatniego) wektora nakładów np. produkcyjności krańcowe wyjdą dodatnie.
W funkcji translog nie jest to możliwe – gdybyśmy chcieli narzucić na parametry warunki zapewniające regularność dla dowolnego wektora nakładów – stracimy własność giętkości (tu muszą mi Państwo wierzyć na słowo – nie będziemy tego dowodzić – ale mogę odesłać do literaturyJ). Więc po oszacowaniu translog może się okazać, że:
Dla niektórych punktów danych elastycznści wychodzą ujemne. Jeśli mamy szczęście, to dla wszystkich danych będzie OK., ale może dla pewnej teoretycznej kombinacji którą chcemy rozważyć (np. odpowiadającej parametrom planowanej fabryki) mogą wyjść ujemne. Dlatego w translogu sprawdzamy np. znaki elastyczności – w punkcie średniej geometrycznej z nakładów (czyli śr. arytmetycznej z logarytmów), potem we wszystkich punktach danych i cieszymy się lub martwimy, ale w ZAWSZE GDZIEŚ w przestrzeni nakładów będą ujemne.
To jest problem – ale zauważmy, że w translogu może on występować z różnym natężeniem – np. możemy w punktach danych mieć wszystko OK. W translogu ponadto zwykle możemy się wybronić w interpretacji, odwołując się do tego, że ma ona tylko zapewnić lokalne przybliżenie i nie wymagamy od niej GLOBALNEJ REGULARNOŚCI.
W CES i CD kiedy wyjdzie nam, że parametry nie spełniają zadanych warunków – to mogiła, bo wtedy funkcja jest nieregularna (nie jest funkcją produkcji) w CAŁEJ PRZESTRZENI NAKŁADÓW.
W związku z tym mamy problem NARZUCANIA WARUNKÓW REGULARNOŚCI EKONOMICZNEJ. Czasem warunki regularności są ewidentnie niespełnione (np. w translogu w większości punktów danych i średniej; w CD i CES jak już są niespełnione, to wszędzie) że nie możemy interpretować naszej funkcji jako funkcji produkcji i wyliczone wielkości nie mają sensu. Możemy próbować je narzucać, ale wtedy jest pytanie od strony statystycznej, o status naszych ocen parametrów w obecności wiążących ograniczeń nierównościowych – to nietrywialne. Te ograniczenia nierównościowe na przestrzeń parametrów dla CES i CD będą proste, ale dla Translog będą funkcją danych (to brzydka strona miłej lokalności charakterystyk) – czyli będą zależały od wszystkich obserwacji – w przestrzeni parametrów może się zrobić wtedy straszna sieczka – i już niezależnie od własności, może się nie dać w ogóle uzyskać ocen.
Więc w CD i CES albo jest wszystko OK. albo do niczego – charakterystyki są globalne lub na tyle mało swobodne, że to na jedno wychodzi – więc i regularność/nieregularność jest globalna; w translog może być różnie – nieregularność może się stopniować – jest trudniejsza do zbadania i do narzucenia, bo jest – jak charakterystyki – lokalna w przestrzeni nakładów. Przypominam i powtarzam, że regularność ekonomiczna jest nam potrzebna, by interpretacja miała sens – nie można tak sobie po prostu napisać zwykłej interpretacji kiedy elastyczność wychodzi ujemna.
Koniec takich
trochę bardziej zaawansowanych rozważań
Funkcja translog (10) ze strukturą stochastyczną i dynamizacją wprowadzoną zgodnie z (6) przyjmie postać:
(11) ![]()
(po wprowadzeniu dynamizacji produkcyjności krańcowe (i tylko one) będą funkcją t i trzeba to uwzględnić w interpretacji i wyliczeniu: interpretacja byłaby taka: Wielkość produkcji wzrośnie w okresie t* o PK* jednostek jeśli wielość nakładu kapitału zwiększy się o 1 jednostkę z poziomu K* przy niezmienionym nakładzie pracy na poziomie L*.)
interpretacja efektu skali byłaby następująca:
Wielkość produkcji w danym okresie wzrośnie o RTS^ % jeśli w tym samym okresie wielość nakładów kapitału i pracy zwiększy się równocześnie o 1% odpowiednio z poziomu K* oraz L*.)
Tutaj fragmenty interpretacji wytłuszczone na czerwono wynikają z własności funkcji Translog, zaś te wytłuszczone na niebiesko – z faktu wprowadzenia dynamizacji.
Równanie (11) daje nam wielkie pole do popisu. Przyjmijmy dla składnika losowego założenia KMNRL i zauważmy, że [por. (4)] funkcja Cobba i Douglasa występuje tu jako szczególny przypadek. Możemy więc rozwinąć wszystkie możliwości wnioskowania opisane w zajęciach 4, zajęciach 5 i zajęciach 6 a w szczególności możemy:
Zadanie
Laboratoryjne
(weźmy dane w postaci szeregów czasowych z pliku maddala.xls) – poziom istotności zostawiamy do zmiany jako parametr, domyślna wartość 0,05)
1) Oszacować funkcję Translog i funkcję C-D – każdą z nich z dynamizacją oraz bez.
2) Wyliczyć oceny elastyczności i efektu skali (w C-D globalne, w translog np. dla wszystkich punktów danych)
3) Testować specyfikację dynamiczną wobec statycznej (test t istotności parametru t)
4) Testować redukcję translog do C-D – test F łącznego zerowania parametrów przy kwadratach i iloczynach logarytmów (na różne sposoby, bo możemy też redukować dynamiczny translog do statycznego C-D)
5) Testować w CD i translog stały efekt skali (RTS=1) – to wnioskowanie o liniowej kombinancji parametrów – zajęcia 6.
6) Budować przedziały ufności dla elastyczności – w CD to po prostu przedziały ufności dla parametrów, w Translog musimy wykorzystać wnioskowanie o liniowej kombinacji parametrów; przedział ufności możemy wyliczyć w każdym punkcie danych lub dla średniej, to samo dla RTS
Wyniki testów proszę przedstawić w postaci p-value.
Proszę następnie zrobić 3 wykresy:
Jeden dla RTS, dwa dla elastyczności.
Na KAŻDYM z tych TRZECH wykresów proszę nanieść W KAŻDYM PUNKCIE DANYCH:
Ocenę punktową danej charakterystyki z funkcji translog i z funkcji C-D +- t alfa razy błąd średni szacunku (czyli będzie 6 linii na każdym wykresie)
Potem proszę zrobić kolejne 3 wykresy, na których porównają Państwo (już bez błędów średnich szacunku) przebiegi Translog zdynamizowany, translog statyczny, C-D zdynamizowany, C-D statyczny (czyli 4 linie na każdym wykresie)
Proszę podpisać wszędzie oś X czyli oś obserwacji numerami lat, a nie numerami t = 1,2 itd.
Dla chętnych – ponad program – jeśli ktoś chce powalczyć
o naprawdę dobrą ocenę (lub po prostu mieć lepszą) to może – w oparciu o zajęcia
6.:
1)
zbudować obszar ufności dla
2 elastyczności w statycznej funkcji C-D.
2)
Zdynamizować tą funkcję, i
ponownie zbudować obszar ufności dla elastyczności
3)
W funkcji zdynamizowanej
zrobić obszar ufności dla RTS i tau.
4)
Przemyśleć rezultaty i mi
pokazać.
Jeśli
ktoś się na to porywa, to miło J – w razie trudności można do mnie mailować.
5)
Może też zrobić obszar
ufności dla RTS i tau lub dla pary elastyczności w Translog, ale tam to będzie
zależało od nakładów – można np. w wybranym punkcie danych i zrobić makro do
przełączania punktów danych – da się JJ.
Podstawowe umiejętności konieczne do rozwiązywania zadań:
- umiejętność wprowadzenia struktury stochastycznej i dynamicznej
- estymacja funkcji C-D i translog oraz wnioskowanie o ich charakterystykach (testy, przedziały ufności) – uwaga! Tu często wchodzi wnioskowanie o liniowej kombinacji parametrów, trzeba się nauczyć robić wektor c dla EL i RTS w translog i RTS w C-D
- wyprowadzenia, wyliczanie wartości i interpretacje (uwaga na poziomy nakładów!) charakterystyk funkcji translog (dla zmylenia w zadaniach funkcja translog bywa podana w postaci „odlogarytmowanej” – trzeba ją zlogarytmować żeby sprowadzić do postaci (10) lub (11)
Ćwiczenia
tablicowe:
Ćwiczymy wyprowadzenia i interpretacje z dynamizacją w CES i funkcją Translog; na sucho pokazujemy jak liczyć błąd średni szacunku efektu skali w C-D i elastyczności w Translog i ew. logarytmu produkcji teoretycznej.
Problem do
przemyślenia na następne zajęcia:
????.